Simulation der Kalksteinkalzinierung in GGR‑Schachtöfen – Einfluss von Herkunft und Größe des Kalksteins
Neben dem Einfluss von Energiezufuhr und Materialdurchsatz sind auch die Herkunft und die Partikelgröße des verwendeten Kalksteins bei der Kalzinierung im GGR-Schachtofen von Bedeutung.
1 Einleitung
Betrieb: Art des Brennstoffes, Energiezufuhr, Luftzahl und Ofendurchsatz
Material: Herkunft, Mittlere Größe, Größenverteilung
Ofen: Art des Ofens, Art der Brennstoffzufuhr, Durchmesser, Höhe
Für unterschiedliche Betriebsbedingungen ist es von Vorteil, das Temperatur- und Konzentrationsprofil im Innern des Ofens zu kennen. Da eine experimentelle Ermittlung dieser Informationen mit einem enorm hohen materiellen und ökonomischen Aufwand verbunden ist, ist es zielführender, mathematische Modelle anzuwenden. Im ersten Artikel wurde ein solches Modell entwickelt, um den Kalkkalzinierungsprozess im GGR-Schachtofen zu beschreiben und die signifikanten Größen wie Kern-/Oberflächentemperatur des Solidpartikels, Gastemperatur, Rest-CO2-Gehalt, Druckverlust entlang der Betthöhe und lokale Wandwärmeverluste zu bestimmen. Aufbauend auf dem ersten Artikel werden weiterführend die wichtigen Einflussparameter Herkunft und Größe der Kalksteine untersucht.
Die Validierung des mathematischen Modells durch Vergleich der Simulationsergebnisse mit gemessenen Temperaturprofilen im Ofen wird in einem nachfolgenden Artikel ausführlich diskutiert.
2 Experimentelle Bestimmung der
Materialeigenschaften
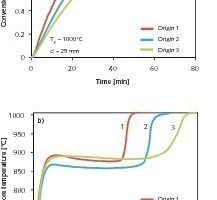
Gemäß Bild 1 wurde der Kalksteinprobekörper so an einer Waage aufgehängt, dass die Masseabnahme und somit der Umsatzgrad kontinuierlich aufgezeichnet werden konnte. Um homogene Strömungsbedingungen um den Probekörper zu realisieren, wird Luft mit einem definierten Volumenstrom vom unteren Ende des Ofens zugeführt. Ein kleines Loch wurde in die Mitte des Probekörpers gebohrt, um anschließend durch Fixierung eines Thermoelementes in diesem Loch, simultan zum Gewichtsverlust, die Temperatur kontinuierlich zu erfassen. Die Kenntnis dieser Kerntemperatur ist dabei elementar für die Analyse der Materialeigenschaften des Kalkes.
Die Messungen wurden mit Zylindern mit Durchmessern von 20 bis 25 mm und Länge-Durchmesser-Verhältnissen von 4 bis 10 durchgeführt. Infolgedessen und durch Isolierung der Zylinder am oberen und unteren Ende können die Proben als unendlich lang und eindimensional betrachtet werden.
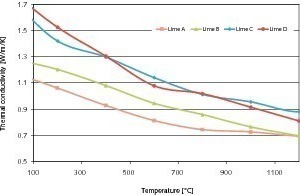
Silva et al. [4] haben die Wärmeleitfähigkeit zersetzter Kalksteinscheiben mit einer Dicke von 3 mm mittels der Laser-Flash-Methode gemessen (Bild 4). Die Wärmeleitfähigkeit verringert sich deutlich mit der Temperatur bis 800 °C, wobei bei Temperaturen über 800 °C die Wärmeleitfähigkeit annähernd konstant bleibt. Sie hängt erheblich von der Herkunft des Steins ab. Bei diesen Messungen variiert die Wärmeleitfähigkeit zwischen 0,7 und 1,0 W/m/K bei Temperaturen über 800 °C.
3 Simulationsergebnisse
Als erstes wurde der Einfluss der Wärmeleitfähigkeit auf den Kalkbrennprozess im GGR-Schachtofen untersucht. Zwei Arten von Kalkstein, die sich ausschließlich durch ihre Wärmeleitfähigkeit unterscheiden, wurden für die Simulation ausgewählt. Während die Wärmeleitfähigkeit des ersten Kalksteins 0,6 W/m/K beträgt, liegt die des zweiten Kalksteins bei 0,8 W/m/K. Der für die Simulation ausgewählte Ofen besitzt die bereits in [1] ausführlich beschriebenen Abmessungen mit einer gesamten Betthöhe von 17 m (6 m Vorwärmzone; 6 m Brennzone; 5 m Überströmkanal und Kühlzone). Die weiteren Ausgangsgrößen zur Simulation sind in Tabelle 1 zusammengefasst.
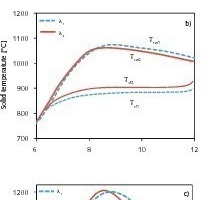
In Bild 5 sind die Massenanteile und Temperaturverläufe in der Brennzone abgebildet. Der Kalkstein 2 mit höherer Wärmeleitfähigkeit wird schneller zersetzt und benötigt demnach eine kürzere Kalzinierungszone. Gemäß Tabelle 2, in der einige wesentliche Simulationsergebnisse aufgelistet sind, verlässt er somit den Ofen mit einem geringeren Rest-CO2-Gehalt. Aus Tabelle 2 wird zudem ersichtlich, dass sich mit einem geringeren Rest-CO2-Gehalt die Temperatur des Abgases und des Kalkproduktes verringert. Begründet wird dies dadurch, dass für einen geringeren Rest-CO2-Gehalt mehr Wärme aus der Verbrennung für die Kalzination verbraucht wird, was schlussfolgernd zu einer geringeren Wärmezufuhr an das Abgas und den Kalk führt.
Zusätzlich sind in Bild 5 die Oberflächentemperatur (Tsw) und die Kerntemperatur (Tsf) der Solidpartikel dargestellt. Für den Zersetzungsvorgang benötigt Kalk mit einer höheren Wärmeleitfähigkeit eine geringere Temperaturdifferenz zwischen Oberfläche und Kern. Folglich resultiert dies in einer höheren Kerntemperatur und einer geringeren Oberflächentemperatur, während die mittlere Temperatur der Kalkschicht annähernd gleich bleibt.
Die Abhängigkeit von Wärmeleitfähigkeit und Oberflächentemperatur ist in einigen industriellen Anwendungen wichtig. Führen chemische Reaktionen an der Kalkoberfläche zur Gasundurchlässigkeit, so führt dies letztlich zum Anhalten des Zersetzungsvorganges. In anderen Fällen kann die Oberflächentemperatur der Kalkpartikel so heiß werden, dass die Oberfläche schmilzt und die Partikel untereinander verkleben können.
Die Verläufe der Gastemperaturen sind für die beiden Simulationsbeispiele im unteren Teil von Bild 5 abgebildet. Im Fall des Kalkes mit höherer Wärmeleitfähigkeit ist dabei die Gastemperatur geringfügig höher. Eine höhere Gastemperatur zusammen mit einem geringeren Rest-CO2-Gehalt (mehr CO2 entsteht in der Gasphase) führt zu einer Erhöhung des Volumenstroms und der Geschwindigkeit des Gases, was wiederum zu einem steigenden Druckverlust im Ofen führt (Tabelle 2).
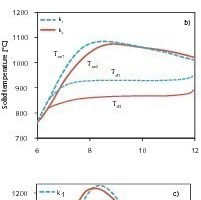
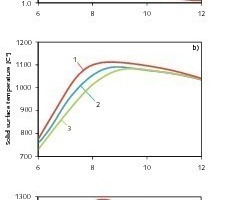
Wie bereits erwähnt, ist der Reaktionskoeffizient ein weiterer dominanter Faktor, welcher den Zersetzungsvorgang beeinflusst. Der Reaktionskoeffizient variiert im Wertebereich von 0,004 bis 0,012 m/s [2,3], wobei die Simulationsberechnungen mit dem niedrigsten und höchsten Wert durchgeführt wurden. Alle anderen Ausgangsgrößen entsprechen den in Tabelle 1 aufgeführten Werten. Bild 6 zeigt im oberen Teil die Simulationsergebnisse für die Umsatzverläufe. Infolge eines größeren Reaktionskoeffizienten steigt die Zersetzungsrate. Hierdurch wird wiederum eine kürzere Kalzinierungszone benötigt und gemäß Tabelle 3 der Rest-CO2-Gehalt reduziert. Des Weiteren zeigt sich in Bild 6, dass der Reaktionskoeffizient die Kern- und Oberflächentemperatur des Solids erheblich beeinflusst. Ein größerer Reaktionskoeffizient benötigt einen niedrigeren Zersetzungsdruck und demnach auch eine geringere Temperatur an der Reaktionsfront. Darüber hinaus zeigt sich, dass durch einen größeren Reaktionskoeffizienten die mittlere Temperatur der Kalkschicht verringert wird, wohingegen im Fall variierender Wärmeleitfähigkeiten die mittlere Kalkschichttemperatur annähernd konstant bleibt.
Bild 6 zeigt, dass der Einfluss des Reaktionskoeffizienten auf das Gastemperaturprofil vernachlässigbar gering ist, da ein größerer Koeffizient lediglich eine vernachlässigbar geringe Erhöhung der Gastemperatur bewirkt. Diese leichte Erhöhung der Gastemperatur hat zusammen mit einem geringeren Rest-CO2-Gehalt einen leicht erhöhten Druckverlust zur Folge.
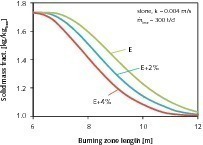
Der aus Kalkstein 3 mit einem geringen Reaktionskoeffizienten gewonnene Kalk verlässt den Ofen mit einem relativ hohen Rest-CO2-Gehalt (3,0 %). Zur Reduzierung des Rest-CO2-Gehaltes können – wie in [1] diskutiert – entweder die Energiezufuhr erhöht oder der Ofendurchsatz verringert werden. In Beispielrechnungen wurde die Energiezufuhr um 2 % und 4 % erhöht.
In Bild 7 sind die Umsatzverläufe und in Tabelle 4 einige wichtige Ergebnisse der Simulationen dargestellt. Der Rest-CO2-Gehalt wird durch Erhöhung der Energiezufuhr erheblich verringert, wobei die maximalen Gas- und Solidtemperaturen sowie auch der Druckverlust wesentlich ansteigen.
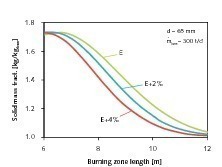
In Bild 8 sind die Umsatzverläufe sowie die Temperaturprofile und in Tabelle 5 die charakteristischen Simulationsergebnisse zusammenfassend dargestellt. Hieraus ist ersichtlich, dass Partikel mit geringerer Größe schneller zersetzt werden, deswegen eine kürzere Kalzinierungszone benötigen und somit einen geringeren Rest-CO2-Gehalt enthalten. Zusätzlich beeinflusst die Steingröße die Länge der Vorwärmzone und die Solidtemperatur. Je größer die Steine sind, desto länger ist die Vorwärmzone und desto geringer ist die Solidtemperatur. Die Verläufe der Gastemperatur sind ebenfalls in Bild 8 dargestellt. Tendenziell entsprechen die Verläufe der Gastemperaturen denen der Solidtemperaturen, somit bewirkt eine geringere Partikelgröße auch eine höhere Gastemperatur, was wiederum zu größeren Gasgeschwindigkeiten führt. Der Druckverlust ist sowohl von der Gasgeschwindigkeit als auch von der Partikelgröße (1/d) abhängig. Mit kleineren Partikeln steigt der Druckverlust maßgeblich an (Tabelle 5).
Im Vergleich der drei Partikelgrößen verlassen die Partikel mit dem größten Partikeldurchmesser (65 mm) den Ofen mit dem höchsten Rest-CO2-Gehalt von 2,3 %. Um diesen Wert zu reduzieren, kann erneut die Energiezufuhr erhöht oder der Ofendurchsatz verringert werden. Beispielhafte Simulationsergebnisse mit erhöhter Energiezufuhr von 2 % und 4 % sind Bild 9 und Tabelle 6 zu entnehmen. Es zeigt sich abermals, dass der Rest-CO2-Gehalt durch Erhöhung der Energiezufuhr erheblich reduziert wird, jedoch dadurch der Druckverlust signifikant ansteigt.
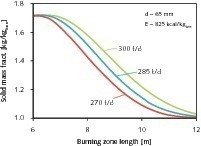
In einer weiteren Simulation wurden Berechnungen mit der Partikelgröße von 65 mm bei reduziertem Ofendurchsatz von 300 t/h, 285 t/h und 270 t/h durchgeführt. Die Ergebnisse sind in Bild 10 und Tabelle 7 dargestellt. Ein geringerer Ofendurchsatz führt zu einer schnelleren Kalzinierungsrate und einer kürzeren Kalzinierungszone, woraus ein geringerer Rest-CO2-Gehalt folgt.
Es ist offensichtlich, dass der Rest-CO2-Gehalt durch Erhöhung der Energiezufuhr und Verringerung des Ofendurchsatzes reduziert werden kann. Jedoch muss dabei stets der Grenzwert des Druckverlustes berücksichtigt werden, denn eine Erhöhung der Energiezufuhr ist nicht möglich, sobald dadurch der Grenzwert des Druckverlustes überschritten wird. In einem solchen Fall kann der Rest-CO2-Gehalt durch Veränderung mehrerer Betriebsparameter verringert werden. So können beispielsweise die Energiezufuhr erhöht und gleichzeitig der Ofendurchsatz verringert werden. Bei der geringsten Partikelgröße von 55 mm wurden entsprechende Simulationen durchgeführt (Tabelle 8) aufgelistet. Im ersten Fall wurde zunächst lediglich die Energiezufuhr erhöht und im zweiten die Energiezufuhr erhöht und gleichzeitig der Ofendurchsatz verringert. Es zeigt sich, dass im ersten Fall der Rest-CO2-Gehalt um 1,2 % reduziert, jedoch der Druckverlust um 25 mbar erhöht wurde, wohingegen im zweiten Fall ein vergleichbarer Rest-CO2-Gehalt bei nur geringem Anstieg des Druckverlustes erreicht wurde.
4 Schlussfolgerungen

tab ZKG KOMBI Test
Es handelt sich hierbei um ein Testangebot. Es berechtigt zu keinem gültigen Abonnement und steht hier rein für Testläufe. Bitte diesem Prozess nicht folgen.
Es handelt sich hierbei um ein Testangebot. Es berechtigt zu keinem gültigen Abonnement und steht hier rein für Testläufe. Bitte diesem Prozess nicht folgen.
tab ZKG KOMBI Study Test
Es handelt sich hierbei um ein Testangebot. Es berechtigt zu keinem gültigen Abonnement und steht hier rein für Testläufe. Bitte diesem Prozess nicht folgen.
Es handelt sich hierbei um ein Testangebot. Es berechtigt zu keinem gültigen Abonnement und steht hier rein für Testläufe. Bitte diesem Prozess nicht folgen.