Simulation der Kalksteinkalzinierung im GGR-Schachtofen – Einfluss der Energiezufuhr und des Durchsatzes

In diesem Artikel wird ein 1-dimensionales mathematisches Modell zur Beschreibung und Simulation des Prozesses der Kalkkalzinierung in einem Gleichstrom-Gegenstrom-Regenerativ-Schachtofen (GGR) vorgestellt. Das Modell beinhaltet ein System aus gewöhnlichen Differentialgleichungen, die aus den Massen- und Energiebilanzen hergeleitet wurden. Daraus lassen sich die Temperaturprofile der Kalkstein-/Kalkpartikel im Schüttbett und der Gasphase entlang der Länge der Ofenachse bestimmen. Die hier dargestellten Berechnungen berücksichtigen die Eigenschaften des Kalksteins/Kalks, da sie einen wesentlichen Einfluss auf den Kalzinierungsvorgang haben. Zusätzlich wird eine Möglichkeit aufgezeigt, den Druckverlust sowie den lokalen Wärmeverlust durch die Ofenwandung entlang der Ofenlänge zu bestimmen. Die Ergebnisse können direkt zur Auslegung, zum Betrieb, zur Regelung und zur Optimierung von GGR Kalköfen genutzt werden.

1 Einleitung

Die ökonomische Situation des industriellen Marktes erfordert die Herstellung des Kalks zu immer geringeren Kosten. Da sich jedoch die Brennstoffkosten, die Anforderungen an die Emissionsreduzierung sowie die einzuhaltenden rechtlichen Maßgaben erhöhen, ergeben sich zwangsläufig höhere Produktionskosten, die der Endverbraucher nicht tragen möchte.

Um sich an die ökonomische Situation anzupassen, beginnen die Kalkhersteller ihre Ofenprozesse durch den Einsatz kostengünstigerer Brennstoffe und Prozessautomatisierung zu optimieren. Die Anlagenbauer hingegen müssen entsprechende Lösungen zur Unterstützung der Ofenbetreiber liefern. Damit eine sichere Entscheidung zur Modifikation der Ofendimensionen oder der Betriebsparameter getroffen werden kann, können Simulationen auf Basis theoretischer Modellvorstellungen genutzt werden.

Es existieren bereits einige Simulationen, die zur Modellierung des Kalkbrennens in verschiedenen Öfen durchgeführt wurden, wie beispielsweise die Modelle von Senegacnik et al. [1] in einem Ringschachtofen, von Shagapov und Burkin [2] in einem Mixed-Feed-Schachtofen und von Piringer und Werner [3] in einem Einzelschachtofen. Ein geeignetes Modell zur Beschreibung des Kalkbrennens in GGR Öfen wurde jedoch noch nicht veröffentlicht. Daher wird nachfolgend ein mathematisches Modell zur Simulation des Prozesses der Kalkkalzinierung in einem GGR Schachtofen vorgestellt. In Abhängigkeit der Kalkstein- und Kalkbeschaffenheit liefert dieses Modell folgende wesentliche Ausgabedaten:

Oberflächen- und Kerntemperaturen der Kalkpartikel

Minimaler Wärmeeintrag und seine Auswirkung auf den Rest-CO2-Gehalt als Qualitätsmerkmal

Maximale Prozesstemperatur als Hinweis für die Belastung des Feuerfestmaterials

Optimierter Durchsatz von bereits bestehenden Öfen und optimierte Höhe der auszulegenden Öfen

Gesamtdruckverlust

Aus den Berechnungen ergeben sich die Temperaturprofile entlang der Ofenachse (eindimensionales Modell). Hierfür werden die Bedingungen im Ofenquerschnitt als homogen angenommen.

Des Weiteren eignet sich das Modell zur Untersuchung der Einflussgrößen: Ofendurchsatz, Ofendimension, Brennstoffart, Luftzahl und Ausbrandkurve des Brennstoffs.

2 Beschreibung der Prozesse

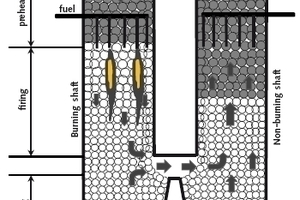
Eine schematische Darstellung des GGR Kalkofens zeigt Bild 1. Der Ofen besteht aus zwei vertikalen Schächten, die über einen Verbindungs-/Überströmkanal miteinander verbunden sind. Die beiden Schächte werden hinsichtlich ihrer Funktionsweise in Brennschacht und Abgasschacht (Nichtbrennschacht) unterschieden, wobei jeder Schacht periodisch jeweils im Brenn- und Nichtbrennmodus betrieben wird. Der Brennmodus (Zufuhr von Brennstoff und Verbrennungsluft) und der Nichtbrennvorgang laufen hierbei simultan.

Während der Brennmodus durch die Gleichstromfahrweise von Verbrennungsgas und Kalkstein gekennzeichnet ist, werden Abgas und Kalkstein beim Nichtbrenn-vorgang gegenläufig geführt. Die Verbrennungsluft wird unter Druck am oberen Ende der Vorwärmzone über der Steinschüttung zugeführt. Das komplette Ofensystem steht dabei unter Druck. Die Verbrennungsluft wird durch den Stein in der Vorwärmzone vorgewärmt, bevor sie sich mit dem Brennstoff vermischt. Vom Brennschacht strömen die Verbrennungsgase durch den Überströmkanal in den nicht brennenden Schacht, wo sie die Wärme während des Nichtbrennvorgangs an den Stein übertragen und dieser die Wärme zur Vorwärmung der Verbrennungsluft für den Brennmodus wieder abgibt. Der regenerative Vorwärmprozess ergibt sich aus der periodischen Abfolge der Wärmeübergänge und liefert den Grund für den geringeren spezifischen Energieverbrauch von GGR Öfen gegenüber anderen Öfen.

Gemäß Bild 1 kann ein Schacht des GGR Ofens prinzipiell in drei Betriebszonen untergliedert werden. Die Vorwärmzone: Der Bereich in dem die Steine Wärme vom Abgas im Nichtbrennmodus erhalten und diese dann für die Verbrennungsluft im Brennmodus regenerieren. Die Brennzone: Der Bereich in dem das Brennstoff-/Luftgemisch verbrannt und der Kalkstein zersetzt wird. Die Kühlzone: Der Bereich in dem der heiße Kalk durch Kühlluft abgekühlt wird.

Der bereits erwähnte Überströmkanal wird zur Verbindung der beiden Schächte sowie zum Transport des Gases vom Brennschacht in den Nichtbrennschacht verwendet.

3. Mathematische Modellierung

3.1 Energiebilanzgleichungen

Der Kalkkalzinierungsprozess in einem GGR Ofen wird durch ein auf der Energie- und Massenerhaltung basierendem Modell beschrieben. Da das periodische Übergangsverhalten (Umsteuerperiode) mathematisch äußerst komplexe Definitionen erfordert und es zudem keine zusätzlichen Informationen zum Prozess liefert, werden nachfolgend mittlere Werte der periodischen Fluktuation unter Vernachlässigung der Umkehrzeit verwendet.

Unter der Annahme stationärer Bedingungen, ergeben sich die Energiebilanzen für das Gas, Abgas und Solid in einem Element der Länge dz aus Gleichung (1)

    (1)

Hierin sind  ·M  der Massenstrom, cp die spezifische Wärmekapazität und T die Temperatur der einzelnen Phase. Zudem sind  · Q i die Wärmeströme durch Konvektion und Leitung zwischen dem Fluid und dem Solid, Δhk die Enthalpie der Zersetzung und d ·M  k die längenbezogene Massenänderung infolge der Reaktion. Die in Gleichung (1) enthaltenen Terme werden für das Gas (g), das Solid (s) und das Abgas (fg) nachstehend erläutert.

Energiebilanz für das Gas

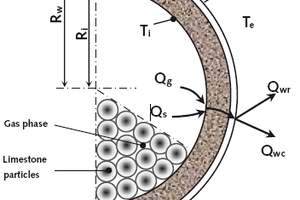
In der Gasphase enthält der Wärmestrom  · Q  g den Wärmeübergang zum Solid  · Q  g↔s und den lokalen Wärmeverlust durch die Ofenwand  · Q  w

    (2)

mit  · Q  g↔s als

    (3)

wobei α der Wärmeübergangskoeffizient, Tsw die Solidoberflächentemperatur, AF die Ofenquerschnittsfläche, O die spezifische Oberfläche der Solidpartikel und ψ der Lückengrad des Bettes ist.

Der Wärmeverlust · Q  w setzt sich aus den Wärmeströmen durch Konvektion  · Q  wc und durch Strahlung  · Q  wr von der äußeren Wandoberfläche zusammen (Bild 2)

    (4)

    (5)

Hierin sind Rw der äußere Ofenradius, αw der konvektive Wärmeübergangskoeffizient von der äußeren Wand zur Umgebung, Tkw die Temperatur der äußeren Wand, Te die Umgebungstemperatur, σ die Stefan-Boltzmann-Konstante, ε der Emissionsgrad der äußeren Wand und Tsk die Temperatur des Weltalls.

Die lokale Reaktionsenthalpie im zweiten Term der Gleichung (1) wird durch die Verbrennung freigesetzt:

    (6)

worin d ·M  f der Brennstoffumsatz und hu der Heizwert des Brennstoffes ist.

Energiebilanz für das Abgas

Der Wärmestrom  · Q  fg beinhaltet den Wärmeübergang zwischen dem Abgas und dem Solid

    (7)

wobei  · Q  fg↔s analog  · Q  g↔s bestimmt wird.

Da keine weiteren Reaktionen stattfinden, wird der zweite Term der Gleichung (1) gleich Null gesetzt.

Energiebilanz für das Solid

Für die Solidphase ergibt sich der Wärmestrom  · Q S aus der Summe der Wärmeübergänge vom Gas  · Q g↔s und vom Abgas  · Q  fg↔s

    (8)

Der Reaktionsterm in Gleichung (1) ergibt sich aus der thermischen Zersetzung des Kalksteins, welche als

    (9)

definiert ist. Hierbei sind ΔhCO2 die spezifische Reaktionsenthalpie bezogen auf das CO2 und d ·M  CO2.L die Zersetzungsrate bezüglich des produzierten CO2Massenstroms, welche detailliert in den nächsten Kapiteln beschrieben werden.

3.2 Massenbilanzgleichungen des CO2

Die Massenströme in den zuvor erwähnten Energiebilanzgleichungen, insbesondere der des CO2, variieren infolge der Kalksteinzersetzung und des Brennstoffumsatzes. Im Brennschacht bestimmt die CO2 Konzentration die Temperatur, die zum Beginn der Kalzination benötigt wird. Das CO2 wird bei der Verbrennung des Brennstoffes sowie bei der Kalzinierung des Kalksteins produziert. In der Brennzone des Brennschachtes ergibt sich daraus die Massenbilanz für das CO2

    (10)

worin  ·M  gf·xCO2f der bei der Verbrennung produzierte CO2 Massenstrom,  ·M  CO2L der bei der Kalksteinzersetzung entstehende CO2 Massenstrom und xCO2.bg die CO2 Konzentration des Gases in der Brennzone ist.

Der Massenstrom des Verbrennungsgases   ·M  gf setzt sich aus den Massenströmen der Verbrennungsluft   ·M  af und dem Brennstoff  ·M  f zusammen

    (11)

Durch den Kalzinierungsvorgang ergibt sich der CO2 Massenstrom entsprechend

    (12)

mit yCO2 als Massenanteil an CO2 im Kalkstein und MLS als Aufgabemassenstrom des Kalksteins.

Aus den Gleichungen (10) und (12) berechnet sich die CO2 Konzentration xCO2.bg in der Brennzone des Brennschachtes.

3.3 Kalksteinzersetzungmodell

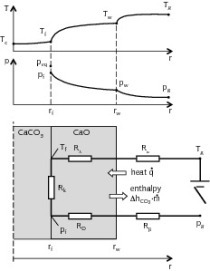
Das Zersetzungsverhalten eines einzelnen Kalksteinpartikels kann über das Kernschrumpfungsmodell entsprechend Bild 3 beschrieben werden, Kainer et al. [5]:

Wärme wird durch Konvektion (α) vom Gas mit der Temperatur Tg auf die Solidoberfläche mit der Temperatur Tsw übertragen und zur Reaktionsfront mit der Temperatur Tsf durch die Kalkschicht geleitet. An dieser wird durch eine chemische Reaktion (k) CO2 abgespalten. Dieses diffundiert mit dem Porendiffusionskoeffizienten (DP) durch die poröse Kalkschicht zur Partikeloberfläche und wird dann konvektiv (β) in die umgebende Gasphase übertragen.

Für die Zersetzung werden ein quasi stationärer Zustand, konstante Materialeigenschaften und kugelförmige Partikel angenommen. Der Wärmestrom durch Leitung von der Partikeloberfläche durch die Kalkschicht zur Reaktionsfront wird beschrieben durch:

    (13)

Der Massenstrom des CO2 infolge der Porendiffusion durch die Kalkschicht und der Konvektion von der Oberfläche zur Umgebung beträgt

    (14)

Der reagierende CO2 Massenstrom ist proportional der Abweichung zwischen dem Gleichgewichtsdruck und dem Partialdruck an der Reaktionsfront

    (15)

wobei für den Gleichgewichtsdruck gilt

    (16)

mit Po=2·15·107 bar und der Reaktionsenthalpie ΔHR=168 kJ/mol bei 900 °C, Silva et al. [7].

Zwischen dem Wärme- und Massenstrom besteht der Zusammenhang

    (17)

Die aus den Gleichungen (13) und (17) hergeleiteten zwei Differentialgleichungen zur Berechnung der Kalzinierungsrate sowie der Kalzinierungstemperatur werden in Kainer et al. [5] sowie Cheng und Specht [6] detailliert beschrieben.

4 Simulationsergebnisse

4.1 Prinzipielle Temperatur- und Umsatzprofile

Den Tabellen 1 und 2 sind die Ofenabmessungen und die Betriebsparameter, die als Ausgangsgrößen zur Simulation dienen, zu entnehmen. Die Ergebnisse der Simulation sind in Bild 4 dargestellt. Der Einfluss der wichtigen Parameter Energiezufuhr und Ofendurchsatz auf den Ofenprozess wird später aufgezeigt. Bezugnehmend auf die schematische Darstellung des GGR Ofens in Bild 1, sind in den Bildern 4a und 4b die entsprechenden Temperaturkurven bzw. Massenprofile in axialer Ofenrichtung abgebildet. Wie zuvor erwähnt, werden im mathematischen Modell die gemittelten Werte der periodischen Fluktuation beschrieben. Demnach stellen die im Bild 4a gezeigten Temperaturprofile die mittleren Temperaturen des Solids, Gases und Abgases dar.

Zunächst wird der Ofen am oberen Ende (0 m) mit Kalkstein bei Umgebungstemperatur von 20 °C beschickt. Der Stein wird vom Abgas im Nichtbrennmodus vorgewärmt. Nach dem Umschalten in den Brennmodus regenerieren die Steine Wärme zur Vorwärmung der Verbrennungsluft. Somit steigen sowohl die Steintemperatur als auch die Lufttemperatur im Bereich der Vorwärmzone. Bei 6 m beginnt die Brennzone, bei der der Brennstoff zugeführt wird. Durch die daraus resultierende Verbrennung des Brennstoff-/Luftgemisches steigt die Gastemperatur. Mit zunehmendem Brennstoffumsatz, steigt die Gastemperatur stärker an, bis diese bei 8,8 m mit 1240 °C ihr Maximum erreicht. Vom Verbrennungsgas wird Wärme an den Stein abgeführt. Die Reaktionstemperatur von 820 °C erreicht der Stein bei 6,3 m, wobei sein Massenanteil ( ·M  g) infolge der CO2 Dissoziation verringert wird, Bild 4b. Weiterhin ergibt sich aus Bild 4a, in dem Bereich 6–7 m, dass die Solidtemperatur geringer als die Abgastemperatur aber immer noch größer als die Gastemperatur ist. Infolge der ansteigenden Verbrennungsrate steigt die Verbrennungsgastemperatur nach 7 m sehr schnell an, so dass das Verbrennungs- und Abgas Wärme auf das Material überträgt. Die Solidtemperatur steigt bis sie größer als die Abgastemperatur ist (8 m). Bis zum Ende der Brennzone (8–12 m) erhält das Solid Wärme vom Verbrennungsgas (im Brennmodus) und führt Wärme an das Abgas (im Nichtbrenn-Modus) ab. Bei 8,8 m erreicht die Gastemperatur mit 1240 °C ihr Maximum, bis aufgrund der verringerten Verbrennungsrate (8,8–12 m), sowohl die Gas- als auch die Solidtemperatur geringer werden. Der Stein verlässt die Brennzone mit annähernd gleicher Oberflächen- und Kerntemperatur und tritt damit in die Kühlzone ein. In diesem Bereich wird durch die Zufuhr von Kühlluft, die Umgebungstemperatur besitzt, die Temperatur des Steins herabgesetzt bis er das untere Ende des Ofens (17 m) erreicht und mit einer Temperatur von 82 °C den Ofen verlässt.

Als wichtige Anmerkung zu Bild 4a sei erwähnt, dass das Abgas im Nichtbrennschacht vom Solid vorgewärmt wird, bevor es den Brennschacht verlässt. Bei einer Ofenhöhe von 8 m erreicht das Abgas dabei Solidtemperatur. Somit überträgt das Abgas Wärme vom Ende des Brennschachtes zum Beginn der Verbrennungszone.

Weiterhin wird aus Bild 4b ersichtlich, dass der Zersetzungsvorgang von 6,3 m bis zum Ende der Brennzone stattfindet, wobei die Zersetzung am Ende der Zone noch nicht abgeschlossen ist. Infolge der Kalksteinzersetzung (dissoziiertes CO2) und der Verbrennung des Brennstoff-/Luftgemisches steigt zudem der Massenstrom des Gases in der Brennzone an. Im Bereich des Überströmkanals wird das Gas mit der vorgewärmten Luft aus der Kühlzone verdünnt und strömt dann als Gemisch/Abgas in den Nichtbrennschacht. Das Abgas verlässt die Vorwärmzone am oberen Ende des Ofens schließlich mit einer Temperatur von 103°C, (Tabelle 3).

Die wesentlichen Ausgabedaten der Simulation wie die Abgastemperatur, die Kalkaustrittstemperatur, die Länge des Kalzinierungsvorganges, der Rest CO2 Gehalt, die maximale Gas- und Solidtemperatur, der Gesamtdruckverlust und die Wärmeverluste durch die Ofenwand sind in ­Tabelle 3 zusammengefasst. Der Wärmeverlust berechnet sich für den betrachteten Fall, bei einer Windgeschwindigkeit wwind = 5 m/s und einer mittleren Temperatur des Weltalls von Tsk = 0 K, auf ca. 6,1 % des Energieeintrags. Dieser Wert hängt von der Art und dem Zustand des verwendeten Feuerfestmaterials (Wärmleitfähigkeit und Dicke), den Wetterbedingungen, die den Wärmeübergang von der äußeren Manteloberfläche zur Umgebung beeinflussen, der Ofengeometrie sowie den Betriebsbedingungen ab (Bild 5). Zusätzlich zu den erwähnten Ergebnissen wurde die Zusammensetzung des feuchten und trockenen Abgases bestimmt und in Tabelle 4 aufgelistet.

4.2 Druckverlustprofil

In der vorliegenden Arbeit wurde der Druckverlust (ΔP) entlang der Länge des Festbettes mit der Gleichung nach Ergun [8] ermittelt.

    (18)

Hierin sind die Gaseigenschaften wie die Geschwindigkeit (w), die Viskosität (ν) und die Dichte (ρ) temperaturabhängig. Der zweite Term dieser Gleichung ist dominant.

Dem Bild 6 ist ein typisches Druckverlustprofil entlang des Ofens zu entnehmen. Die Berechnungen wurden mit einer Partikelgröße von 60 mm und einem mittleren Lückengrad des Ofens von 0,38, welcher sich aus den Berechnungen nach Tsotsas [9] ergibt, durchgeführt. Wie zuvor simuliert wird die Temperaturabhängigkeit der Gaseigenschaften berücksichtigt. Bedingt durch die geringe Gasströmung, ist der Druckverlust in der Kühlzone mit ΔP < 5 mbar relativ klein. Die Druckverlustberechnungen der Vorwärm- und Brennzone werden für beide Schächte durchgeführt. Es ist ersichtlich, dass der Gesamtdruckverlust der beiden Schächte ca. 340 mbar beträgt, wobei sich der Druckverlust im Brennschacht auf etwa 120 mbar und im Nichtbrennschacht auf etwa 220 mbar beläuft. Der größere Druckverlust im Verhältnis zum Brennschacht ist auf die deutlich größere Gasströmung im Nichtbrennschacht zurückzuführen. Die große Gasströmung wiederum ergibt sich aus dem zugeführten CO2 des Kalksteins, der Kalkkühlluft sowie der Lanzenkühlluft.

5 Einflussparameter

5.1 Einfluss der Energiezufuhr

Es wurden drei Simulationen mit variierender Energiezufuhr von E = 825 ± 15 kcal/kglime, bei konstanten Eingabeparametern entsprechend den zuvor erwähnten standardisierten Bedingungen, durchgeführt. Die resultierenden Profile der Oberflächentemperatur der Partikel und des Kalksteinumsatzes in der Brennzone sowie die weiteren Ergebnisse sind den Bild 7 und der Tabelle 5 zu entnehmen. Eine größere Energiezufuhr führt zu einer höheren Wärmefreisetzung durch die Brennstoffverbrennung und somit zu höheren Temperaturen der Steine und des Gases, Bild 7a. Die Gas-temperatur ist aus Gründen der Übersichtlichkeit im Bild nicht enthalten. Bei einer Energiezufuhr im Bereich von 810 bis 840 kcal/kglime reicht die durch die Verbrennung freigesetzte Energie nicht zur vollständigen Kalzinierung des Kalksteins aus. Somit enthält der produzierte Kalk eine gewisse Menge an nicht zersetztem Kalkstein und damit einem Rest CO2 Gehalt, wie es in Bild 7b und der Tabelle 5 abgebildet ist. In Tabelle 5 zeigt sich weiterhin, dass durch eine erhöhte Energiezufuhr die maximale Gas- und Solidtemperatur ansteigen und der Rest CO2 Gehalt im Kalk verringert wird. Zudem erhöhen sich dadurch die Kalkaustritts- und die Abgastemperatur an den beiden Enden der Öfen. Andererseits führt eine Erhöhung der Energiezufuhr zu einem Anstieg der Gasströmung, -temperatur und -geschwindigkeit, wodurch ein größerer Druckverlust entsteht.

5.2 Einfluss des Kalkdurchsatzes

Um den Einfluss des Kalkdurchsatzes auf die Ofenleistung zu untersuchen, wurden drei Simulationen im Bereich von 300 ± 20 t/d durchgeführt. Die Simulationsergebnisse können Bild 8 sowie der Tabelle 6 entnommen werden. Mit steigendem Durchsatz verringert sich die Verweilzeit des Solids im Ofen. Demnach kann dem Solid weniger Wärme vom Gas zugeführt werden und es kommt entsprechend Bild 8a zu einer Verringerung der Temperatur des Schüttbettes. Die Solidtemperatur beeinflusst die Position der Kalzinierungszone und den Umsatzgrad (Bild 8b). Wenn die Gleichgewichtstemperatur zur Kalzinierung erreicht ist, beginnt der Zersetzungsvorgang. Somit ist die Position des Solids zum Erreichen der Gleichgewichtstemperatur abhängig von der Durchsatzrate. Je höher der Kalkdurchsatz ist, desto mehr verzögert sich die Kalzinierungszone (Bild 8b) und umso höher ist der Rest CO2 Gehalt (Tabelle 6). Der Anstieg des Rest CO2 Gehalts führt zu höheren Abgas- und Kalkaustrittstemperaturen. Dies ergibt sich daraus, dass die nicht zur Kalzinierung genutzte Wärme direkt an das Abgas und den Kalkaustritt abgegeben wird. Weiterhin resultiert aus einem höheren Kalkdurchsatz ein Anstieg der Gasströmung und folglich ein größerer Gesamtdruckverlust des Ofens.

6 Schlussfolgerungen

Mit dem stationären eindimensionalen mathematischen Modell kann der Prozess des Kalkbrennens in einem GGR Ofen beschrieben werden. Die Temperaturen des Solidkerns und der Solidoberfläche, die Gastemperatur, die Zersetzungsrate des Kalksteins, der Wärmeverlust durch die Ofenwand und Druckverlust entlang der Höhe des Ofens kann in Abhängigkeit der Betriebsbedingungen simuliert werden. Das Modell hilft dabei den komplexen Prozess in Kalkschachtöfen zu verstehen und liefert eine kostengünstige Basis zur Optimierung der Betriebsbedingungen und zur Auslegung von GGR Öfen in der Praxis (Bild 9).

Eine höhere Energiezufuhr führt dabei zu einem Anstieg der Gas- und Solidtemperatur und einem verringerten Rest CO2 Gehalt im Kalk. Bei einem erhöhten Kalkdurchsatz verringert sich zum einen die Solidtemperatur und zum anderen erhöht sich der Rest CO2 Gehalt sowie der Druckverlust im Ofen. Zur Reduzierung des Rest CO2 Gehaltes muss folglich entweder die Energiezufuhr erhöht oder der Kalkdurchsatz verringert werden. Um höhere Temperaturen im Ofen und damit härter gebrannten Kalk zu erzeugen, muss also der spezifische Energieeinsatz erhöht oder der Durchsatz verringert werden.

Der Einfluss der Kalksteinherkunft und der Größe der Partikel sowie eine Validierung der Temperaturprofile durch Messungen an einem industriellen GGR Ofen werden in späteren Veröffentlichungen präsentiert.