1 Einleitung
Zement wird aus Gips und Klinker gemahlenem, der aus einer Mischung von Kalkstein und Ton in einem bestimmten prozentualen Verhältnis gebrannt wird. Der Drehrohrofen ist das Kernstück eines Zementwerks, in dem Klinker produziert wird. Zement ist ein wichtiges Material für das Bauwesen. Die Chemie der Zementherstellung wurde schon detailliert untersucht (Bogue 1995, Lea 1956). Die Leistung der Zementindustrie steht im direkten Zusammenhang mit dem Baugeschäft im Allgemeinen und ist somit ein Zeichen für die wirtschaftliche Gesamtsituation in einer Region oder in einem Land (Laszlo, Ignacio, Antonio, Peter 2008).
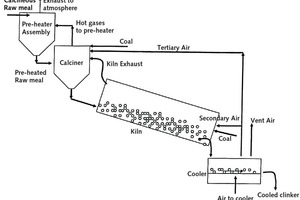
Drehrohröfen produzieren über den Wärmeprozess Klinker, der für die Herstellung von Portlandzement und anderen Arten von hydraulischem Zement eingesetzt wird. Dabei reagiert Kalziumkarbonat mit siliziumdioxidhaltigen Materialien, um eine Mischung von Kalziumsilikaten zu bilden. Jährlich werden mehr als 1 Mrd. t Zement hergestellt und Drehrohröfen sind das Kernstück in diesem Produktionsprozess. Ihre Kapazität wird im Allgemeinen von der Ofenkapazität begrenzt. Als wichtigster Energieverbraucher und Treibhausgasemittent ist es das Hauptanliegen der Zementindustrie, die Effizienz zu steigern (Blezard 1998). Bild 1 zeigt schematisch den Brennprozess in einem Zementwerk.
2 Drehrohrofenmantel
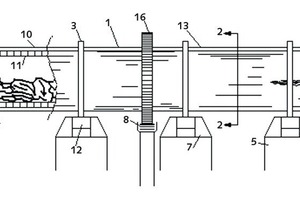
Tabelle 1 zeigt die Mantelstärke der einzelnen Hüllenabschnitte des Drerohrhofens im Zementwerk Darab (DCF). Die Null befindet sich dabei am oberen Ende des Drehofens mit der Bezeichnung „amont“. Die Abstände zwischen den Lagerungen sind in Millimetern angegeben und kennzeichnen das untere Ende des Drehofens. Bild 2 zeigt die Seitenansicht der Ausführung eines Drehrohrofens, der in Übereinstimmung mit dem gegenwärtigen technischen Stand gefertigt wurde. Teilweise wird das Innere des Ofens gezeigt (Davis 1924; Redgrave, Spackman, 2010; Pazand, ShariatPanahi, Pourabdoli, 2009).
Erläuterung: Bild 2 zeigt den Drehrohrofen (1) zusammen mit den Teilen, die ihn um seine Längsachse drehen (3), (12), (8) und (16). Zum Ofen (1) gehören ein länglicher, zylindrischer, sich drehender Mantel (13), der Ofeneinlauf (9), der gegenüberliegende Ofenauslauf (6) und ein Brennerrohr (4). Der Ofen (1) wird so montiert, dass der Ofenauslauf (6) niedriger liegt als der Ofeneinlauf (9), so dass das Material (15) durch wandern kann. Es läuft durch die offene Brennzone zum Ofenauslauf (6). Der Ofenmantel (13) ist auf Laufringen (3) gelagert, die auf Stahlrollen (12) laufen, die wiederum von Betonpfeilern (5) und einem Stahlrahmen (7) getragen werden.
3 Darstellung des Algorithmus
Der Algorithmus des Rechnenprogramms beruht auf Informationen über die äußere Manteltemperatur, die man durch Messungen der Temperaturscanner erhält. Die erfassten Ofenmanteldaten werden zusammen mit dem berechneten Temperaturprofil des Gasstroms im Ofeninneren und einer Simulation des Ofenmodells für die Berechnung der Ansatzstärke herangezogen. Den für diesen Artikel verwendete Algorithmus lieferten Berechnungen für bestimmte Stellen im Ofen, an denen die blanken Steine der Ausmauerung dem heißen Gasen ausgesetzt sind. Das konzipierte Programm berechnet an dieser Stelle eine dünnere Steinstärke anstelle der Ansatzstärke und sichert diese Informationen zum betreffenden Punkt für weitere Anwendungen im Ofenbetrieb.
Nach dieser Methode hängt die Ansatzstärke nicht nur von der Außenmanteltemperatur ab, sondern auch von den Betriebsbedingungen, die sie beeinflussen. Um die Ansatzstärke aus den Wärmeübergangsbeziehungen durch den zylindrischen Wärmewiderstand rund um den Ofen festzustellen, ist es vorrangig erforderlich, die Temperaturprofile der Materialien im Ofen zu bestimmen. Das kann erreicht werden, indem ein Modell des Ofens im DCF im Ruhezustand simuliert wird.
In der Literatur findet man zu Drehrohröfen verschiedene Modelle. Sie basieren auf unterschiedlichen Annahmen und führen zu Modellen in unterschiedlichen Qualitäten. Neben der Stabilität der Bauteile berücksichtigen die Modelle Massen- und Energiebilanzen. Auch ein Flammenmodell ist ein wichtiger Teil des Gesamtmodells des Ofens. Ein dynamisches Modell kann zur Simulation der Ofendynamik eingesetzt werden. Jedoch ist bei diesem Rechenprogramm zum Ofenansatz ein Modell im Ruhezustand ausreichend, und man zieht es vor, sich nicht mit der Dynamik des Ofens zu befassen, während die Simulation durchgeführt wird. Das ist darauf zurückzuführen, dass die Laufzeit für die Ofensimulation viel geringer ist als die Dynamik des Ofens und die der Ansatzschwankungen. Auch in Situationen, wenn der Ansatz nicht hält – was zu plötzlichen Änderungen der Ansatzstärke in einer beträchtlichen Größenordnung führt – ist die Dynamik des Wärmeübergangs durch den zylindrischen Wärmewiderstand so viel langsamer festzustellen als aus den Schwankungen der Ofenmanteltemperatur. Daher ist es zur Beschleunigung der Berechnungen viel sinnvoller, ein Modell im Ruhezustands als ein dynamisches zu verwenden. In den folgenden Abschnitten werden nach einer kurzen Diskussion zum eingesetzten Ofenmodell die Beziehungen für den Wärmeübergang in mehrschichtigen zylindrischen Wänden dargelegt.
Die in diesem Programm verwendeten Informationen und Daten entsprechen den Ofenkenndaten in diesem Artikel. In dieser Software werden die Inputdaten online von SCADA-Signalen von den Messfühlern zum Computer übertragen. Einige Daten sollten dem Computerprogramm im „Offline“-Modus zugeführt werden. Beide Formen werden auf dem Monitor für den Betreiber angezeigt.
4 Analyse des Ofenmodells
Die Modellierungsanforderungen der Software zur Bestimmung der Ansatzstärken können in zwei Teile aufgeteilt werden. Eines ist ein Modell für die Simulation, die man vom Temperaturprofil des Gasstroms im Ofen erhalten hat. Das andere ist ein Modell des Wärmeübergangs durch die benachbarten zylindrischen Schichten um den Ofen herum. Das Modell des Zementdrehrohrofens ist in der Tat hochgradig nichtlinear. Es gibt diesbezüglich zahlreiche Modelle in der Literatur.
Das Modell von Spang (1972) ist ein dynamisches Differenzmodell, das man aus den Masse- und Energiebilanzen des Mantels über eine unterschiedliche Länge bei Grenzbedingungen am Ofenein- und -auslauf erhielt. Für die erforderlichen Ziele des Schätzens der Ansatzstärke ist es gut anwendbar in seiner Version des Beharrungszustands. Das Modell von Spang kann für die Simulation eingesetzt werden, die man aus den Temperaturprofilen des Gases, der Feststoffe und der Wandung entlang des Ofens erhält. Einen Nachteil hat das Modell von Spang jedoch: das Flammenmodell.
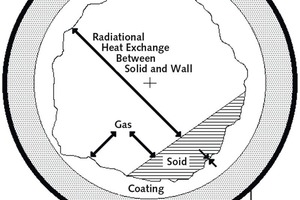
In dem Algorithmus des Computerprogramms wurde das Flammenmodell von Gorog (Gorog, Brimakombe, Adams 1983) verwendet. Die Simulation des Modells von Spang führt zu einem durchschnittlichen Temperaturprofil der Mantelstärke sowie des festen Materials und des Gases entlang des Ofens. Die erhaltenen Temperaturprofile in Kombination mit den Scannermessungen der Manteltemperatur können für eine Einschätzung der Ansatzstärke über ein geeignetes Wärmeübergangsmodell durch die benachbarten zylindrischen Widerstände des angenommenen Ofens verwendet werden. Bild 3 zeigt die verschiedenen Arten des Wärmeübergangs im Innern des Ofens zwischen Gas, Feststoff und Wand.
Nach diesem Schema wurde die Modellierung des Beharrungszustands des Ofens für die Bestimmung der Temperaturprofile mit folgenden Annahmen durchgeführt:
Man geht davon aus, dass die spezifische und die Reaktionswärme unabhängig von der Temperatur sind, und dass sie in axialer Richtung konstant sind.
Die Leitung in Gasen und Feststoffen in axialer Richtung wird vernachlässigt.
Die Koeffizienten der Konvektion und Abstrahlung werden als unabhängig von der Temperatur und Position betrachtet.
Die Höhe und Geschwindigkeit der Feststoffe werden in jedem Querschnitt des Ofens als konstant angenommen. Der Transport von Feststoffen durch den Gasstrom wird vernachlässigt. Dann können die Reaktionsgeschwindigkeiten durch das Arrhenius-Gesetz bestimmt werden.
Das in den Gasstrom aus der Kalzinierreaktion eintretende H2O und CO2 wird in den Massebilanzen dieser Komponenten vernachlässigt.
Um einige Verbesserungen in der Simulation zu erreichen, wurde das Flammenmodell von Gorog (Gorog, Adams, Brimakombe 1983, Gorog, Adams, Brimakombe 1982) anstelle des Flammenmodells von Spang (Spang 1972) verwendet. Das Flammenmodell von Gorog bestimmt die Länge der Flamme. In diesem Modell hat die Flamme eine deterministische Länge, die vom Brennstofftyp, der Temperatur der Sekundärluft, der Menge der zusätzlichen Luft und der Durchflussmenge des Brennstoffs abhängt. Im Flammenmodell von Gorog wird angenommen, dass die Strahlungsenergie nicht durch die benachbarten Elemente geht und in jedem Element zwischen den Phasen ausgetauscht wird. Diese Annahme impliziert natürlich, dass der Wärmeübergang in axialer Richtung in der Flamme ignoriert wird.
4.1 Masse- und Wärmebilanzen des Ofens
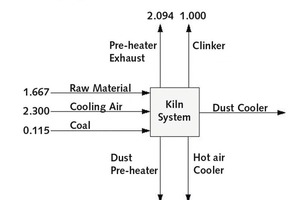
Bild 4 zeigt das Klinkerinputverhältnis von Rohmaterial, Kühlluft und Kohle in der Ofenanlage. Das Rückführungsverhältnis von Input und Output ist gleich. Die Eintragswerte des Rohmaterials in den Ofen des DCF, der Kühlluft und der Kohle betragen 1,667, 2,300 bzw. 0,115 kg/kg Klinker. Der durchschnittliche Eintragswert beträgt 4,082 kg/kg Klinker. Andererseits wird das Ausbeuteverhältnis in fünf Bereiche unterteilt. Der erste ist die Entlüftung des Vorwärmers (2,094 kg), der zweite ist der Klinker (1,00 kg), der dritte ist der Heißluftkühler (0,940 kg), der vierte ist der Staubvorwärmer (0,042 kg), und der fünfte ist der Staubkühler (0,006 kg). Dieser Durchschnitt ist auch beim Inputwert gleich (4,082 kg/kg Klinker). Eine große Menge von Klinker wird jedoch im Absaugteil des Vorwärmers genutzt. Nur 1,8 % Sauerstoff, 27,4 % CO2 und ein Maximum von 70,8 % Stickstoff werden in der Absaugung des Vorwärmers genutzt. Dieses System nennt man „Massebilanz des Ofens“.
Für die Energiebilanz wird in dem Modell eine durchschnittliche Gesamtwandtemperatur verwendet. Die erforderlichen Gleichungen (1) bis (3) beziehen sich auf Gas, Feststoff bzw. Wand (Spang 1972).
Wärmebilanz der Gasphase:
AgCpgrgvg ∂Tg = b1 (Tw – Tg) + b2(Ts – Tg) + Qcomb⇥(1)
∂z.
Wärmebilanz der Feststoffphase:
AsCpsrsvv ∂Ts = b2 (Tg – Ts) + b3(Tw – Ts) + AsQcomb⇥(2)
∂z.
Wärmebilanz der Wand:
b1(Tg – Tw) + b3(Ts – Tw) + B4(Ta – Tw) = 0⇥(3)
Die Wärme der Reaktion wird berechnet als:
QC = rs [– ∆Hzk1 z – ∆HvRv –
⇥∆Hbkb S(C)2 – ∆HakaCb] (4)
(1 + Ai + Fi + Si)
(b1, b2, b3, b4) sind nichtlineare Funktionen von Temperaturen, der Konvektion sowie Koeffizienten und die Geometrie des Wärmeübergangs der Strahlung. Sie können mit den Gleichungen (5) bis (8) berechnet werden.
Koeffizient des Wärmeübergangs zwischen den Gasen und der Innenwand:
b1 = 1.7307r1 p[ƒ1 + 1.73*10-9 (1 – ho) «g«w(Tg2 – Tw2) (Tg + Tw)] (5)
Koeffizient des Wärmeübergangs zwischen den Gasen und dem Feststoff:
b2 =
3.4314r1 sin (P – 2 ) [ƒ2 + 1.73*10-9 (1 – ho) «g«s(Tg2 – Tw2) (Tg + Ts)] (6)
Koeffizient des Wärmeübergangs zwischen der Wand und dem Festsstoff:
b3 = r1 (2π – p) [ƒ3 + 1.73*10-9 h «w«s(Ts2 – Tw2) (Ts + Tw)]⇥(7)
Koeffizient des Wärmeübergangs zwischen der Außenwand und der Umgebungstemperatur des Feststoffs:
b4 = 2π ƒ4 r2⇥(8)
Für die Berechnung des Koeffizienten des Wärmeübergangs zwischen der Wand und der Umgebung (Außenluft) wurde in der vorangegangenen Arbeit (Gorog 1982) die Gleichung (8) verwendet. Die Gleichung (8) ist eine grobe Beschreibung des Koeffizienten des Wärmeübergangs zwischen der Manteloberfläche und der Umgebung, die Gorog (1982) verwendet. Da in dieser Gleichung im Ofen konstant ist, ist in dieser Gleichung nicht gegenüber den Bedingungen in Längsrichtung empfindlich. Um die Genauigkeit des Modells zu erhöhen, wurde der Koeffizient des Wärmeübergangs des Außenmantels als Summe der konvektiven und der strahlenden Koeffizienten des Wärmeübergangs der Außenwand von Gorog (1982) und Gorog, Adams, bzw. Brimakombe (1983), angenommen.
hcv, shl—a = 0.11kaPr0.36 (0.5 Rev2 + Re2 + Gr)0.35⇥(9)
D........
hRsh→a = C`«shsTsh3⇥(10)
Wobei in Gleichung (10):
C` = {1 + Ta + ( Ta )2 + ( Ta )3} ⇥(11)
Tsh Tsh
Tsh
Aus Gleichung (10) folgt, dass hcv, shl—a von der Temperatur abhängig ist, weil Pr, Re und Gr stark von den Umweltbedingungen beeinflusst werden. Um das Modell zu verbessern, wurde daher zuerst die Manteltemperatur über die Ofenlänge von einem Scanner der Manteltemperatur aufgezeichnet. Dann wurden die dimensionslosen Gruppen in Gleichung (11) entsprechend der Folientemperatur (Durchschnittstemperatur von Mantel- und Lufttemperaturen) über die Ofenlänge berechnet. So kann der Wert hcv, shl—a in jedem Längsschnitt entlang des Ofens berechnet werden. Da die Manteltemperatur mit der Zeit schwankt, und diese Schwankung prompt das Modell beeinflusst, kann man sagen, dass die Erscheinungen des Wärmeübergangs in den Modellen einigermaßen quasi-dynamisch sind. Diese algorithmische Methode gestattet es, die Schwankungen im konvektiven Wärmeübergangskoeffizienten als eine abhängige Größe sowohl von der Zeit als auch vom Längsabstand zu berücksichtigen.
Die Massebilanzen (12) und (13) gelten für die zehn Feststoffkomponenten, die in den Reaktionen in Zementöfen vorkommen, und für die Gaskomponente (CO2).
Ri = vs ∂Ci ⇥(12)
∂z.
Rj = vg ∂Cj ⇥(13)
∂z.
wobei i: H2O, CaCO3, SiO2, Al2O3, Fe2O3, CaO, C3S, C2S, C3A, C4AF und j: CO2.
Alle Koeffizienten und Konstanten wurden im Anhang 1 zusammengefasst.
5 Flammenmodell
Wie bereits erwähnt, wurde für den Drehrohrofen ein Pfropfenströmungsmodell (Gorog, Adams, Brimakombe, 1983) verwendet. Bei diesem Modell wurde die Flammenzone in „n“ Scheiben gleicher Größe unterteilt. Die Stärke jeder Scheibe ist gleich für die Schrittgröße des mathematischen Gleichungslösers, was später diskutiert wird.
Die Anzahl der Scheiben wurde berechnet als:
n = FL ⇥(14)
Simulation Schrittweite
Die gesamte Flammenlänge FL erhielt man aus der Gleichung von Beer (Gorog, Adams, Brimakombe, 1983):
FL = 6do (1 + AF*) ( re )0.5 ( re )0.5⇥(15)
rse rse
In der Arbeit von Gorog wurde der Ofen mit einem Doppel-Koaxialbrenner (Gorog, Adams, Brimakombe, 1983) ausgestattet:
re = mF + mpa⇥(16)
mƒ mpa
rF + rpa
do = mF + mpa ⇥(17)
[(GF + Gpa) πre]0.5
AF* = AF mF – mpa⇥(18)
mF .
Alle Koeffizienten, Konstanten und Bezeichnungen sind im Anhang 1 zusammengefasst.
Entsprechend der vorherigen Untersuchungen (Gorog 1982) stimmt die Vorhersage der Gleichung (15) mit den Flammen innerhalb von 20 % der tatsächlichen Werte weitgehend überein.
Die Werte von mF und msa konnten instrumental am Drehrohrofen aufgezeichnet werden. Der Wert mpa wurde berechnet, weil man msa kannte und der Luftüberschuss für den Brenner zwischen und 10 und 15 % liegt.
Die erforderlichen Parameter des untersuchten Brennstoffs sind im Anhang 1 enthalten. Auch GF und Gpa in Gleichung (17) stehen für die verzögerungsfreie Durchflussmenge des Brennstoffs bzw. der Primärluft, die mit Hilfe der Durchmesser des Koaxialbrenners berechnet wurde, die in Anhang 1 enthalten sind.
Jetzt wurde Qcomb in Gleichung (1) mit folgendem Ausdruck berechnet:
Qcomb = mƒ *LHV + mpa *Gpa *(Tpa – Tref) + msa *Gpsa *(Tsa – Ta)
Simulation Schrittweite⇥(19)
Um einige Verbesserungen in der Simulation zu erreichen, wurde das Flammenmodell von Gorog anstelle des Flammenmodells von Spang verwendet. Das Flammenmodell von Gorog bestimmt die Länge der Flamme. Im Flammenmodell von Gorog hat die Flamme eine deterministische Länge, die vom Brennstofftyp, der Temperatur der Sekundärluft, der Menge der zusätzlichen Luft und der Durchflussmenge des Brennstoffs abhängt. Im Flammenmodell von Gorog wird angenommen, dass die Strahlungsenergie nicht zu den benachbarten Elementen vordringt und zwischen den Phasen in jedem Element ausgetauscht wird. Diese Annahme bedeutet, dass der Wärmeübergang in axialer Richtung in die Flamme ignoriert wurde.
6 Modellierung des Wärmeübergangs von der Wand
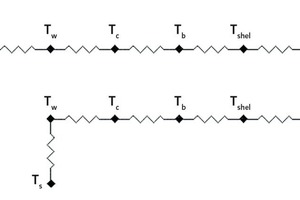
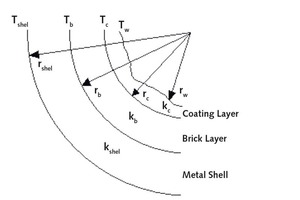
Durch den Einsatz der Wärmeübergangsbeziehungen durch die benachbarten zylindrischen Schichten mit Hilfe der Messungen der Außenmanteltemperatur und der simulierten Innentemperaturprofile ist es möglich, die Ansatzstärke zu berechnen. Bild 5 zeigt zwei Arten der Widerstandsnetzwerke des Wärmeübergangs, die für den Wärmeübergang vom Innern des Ofens an die Umgebung berücksichtigt werden können. In Bild 5a wird gezeigt, dass eine Reihe von Widerständen für die Darstellung des Wärmeübergangs von den Heißgasen zur Umgebungsluft verwendet werden kann. Diese Art von Netzwerk kann für die Oberfläche im Ofen verwendet werden, wo die Heißgasse mit der Oberfläche des Ansatzes in Berührung kommen (Bokaian 1994). Für die Flächen, wo der Ansatz mit dem Feststoff in Berührung kommt, kann das Widerstandsnetzwerk entsprechend Bild 5b gezeigt werden. Das ist so, weil der Feststoff die Wärme von den heißeren Ansatzoberflächen erhält. Als Ergebnis entsprechen die zylindrischen Wärmeübergangsbeziehungen Bild 5b, wenn die Messungen der Manteltemperatur in einem bestimmten Winkel zur Lage des Feststoffs durchgeführt werden. Wenn die Messungen in einem Winkel entsprechend der Gasphase durchgeführt werden, trifft Bild 5a zu. Die in den Wärmeübergangsgleichungen verwendeten Symbole werden in Bild 6 gezeigt.
Bild 6 zeigt die unterschiedlichen benachbarten zylindrischen Schichten, in denen der Wärmeübergang stattfindet. Die folgenden Annahmen werden für die Modellierung des Wärmeübergangs von den zylindrischen Schichten getroffen.
Es wird ein einheitlicher Wärmeübergang von den zylindrischen Schichten angenommen.
Der Wärmeübergang in axialer Richtung wird ignoriert.
Temperaturschwankungen von winkligen Wänden werden vernachlässigt.
In den Widerstandsschichten gibt es keine Wärmeerzeugung.
Entsprechend Bild 6 haben die unterschiedlichen Schichten folgende Grenzbedingungen:
Ansatzschicht
at r = rw T = Tw & at r = rc T = Tc⇥(20)
Schicht der feuerfesten Auskleidung
at r = rc T = Tc & at r = rb T = Tb⇥(21)
Schicht des metallischen Mantels
at r = rb T = Tb & at r = rshl T = Tshl⇥(22)
Unter Verwendung der grundlegenden Gleichung (23) für den konduktiven Wärmeübergang können die Wärmeübergangsgleichungen in den Schichten als die Gleichungen (24) bis (26) in zylindrischen Koordinaten ausgedrückt werden
QT = –kA ∂T ⇥(23)
∂r.
QT = 2π ∆z kc(Tw – Tc)⇥(24)
1n (rc/rw)
QT = 2π ∆z kb(Tc – Tb)⇥(25)
1n (rb/rc)
QT = 2π ∆z kshl(Tb – Tshl)⇥(26)
1n (rshl/rb)
Die zu berechnende erforderliche Ansatzstärke beträgt an jeder Stelle:
d = rc – rw⇥(27)
Der Wärmestrom durch die Wärmewiderstände und seine Übertragung in die Umgebung ist eine Funktion der äußeren Oberflächentemperatur der metallischen Wand (Tshl) und kann mit Hilfe der Gleichung (28) in jedem Ofenschuss festgestellt werden:
QT = 2π ∆z rshl hshl – a (Tshl – Ta)⇥(28)
7 Allgemeine Vorstellung für die Durchführung
Auf dem Bildschirm erscheint ein Bild eines Ofens und ein langes Diagramm, das den Moment der minimalen Stärke des Ansatzes in jedem Abschnitt zeigt, sowie ein Diagramm, das die durchschnittliche Stärke des Ansatzes in unterschiedlichen Abschnitten darstellt. Auch können Informationen zu den Berechnungen und Inputdaten sowie über Veränderungen der Stärke der feuerfesten Auskleidung zu unterschiedlichen Zeitpunkten in einem Computer ausreichend lange gespeichert werden. Bei einer konventionellen Schätzung wird nur die Hauttemperatur gemessen und die Ansatzstärke nach dem Angebot des Nutzers vorhergesagt.
Die Temperaturdaten des metallischen Mantels sind an unterschiedlichen Stellen durch Messungen mit einem Scanner außerhalb der Anlage zugänglich. Diese Informationen werden zusammen mit den anderen Daten der Input- und Outputgrößen des Ofens zum Computer übertragen, der sich im Leitstand befindet.
Unter Verwendung der Input- und Outputgrößen kalkuliert das Rechenprogramm die momentane Gastemperatur an den unterschiedlichen Innenteilen des Ofens (Pisters, Beeke 1985; Schubin, Gnerdia, Sokolinkaja 1985). Die berechnete Temperatur ermöglicht zusammen mit der gemessenen Temperatur des metallischen Mantels die Berechnung der Ansatzstärke, indem die Gleichungen des Wärmeübergangs in den mehrschichtigen zylindrischen Wänden verwendet werden.
Die Berechnung des Gasprofils entlang des Ofens erfordert mit Hilfe der gemessenen Input- und Outputgrößen des Ofens, wie z.B. Temperatur, Gas- und Brennstoffdurchflussmenge sowie auch die Dichte der Teile und die wesentlichen Oxide des Ofenbrennstoffs, ein mechanisches Modell auf der Grundlage einer Masse- und Temperaturbilanz in Längsrichtung in einem anderen Element (Noshirvani 2006).
Durch Lösung dieses Modells und auch des Flammenmodells erhält man das Material- und Wandtemperaturprofil im radialen und winkeligem Schnitt, sowie das Profil der Gastemperatur. Durch die Berechnungen des Wärmeübergangs von der Wand, die für die Ansatzstärke verwendet und in Radialrichtung modelliert wird, erhält man die Durchschnittstemperatur der Wand.
8 Physikalische Struktur und Lastmessung
Die unterschiedlichen chemischen, mechanischen und thermischen Erfordernisse der einzelnen Ofenschüsse können unterschieden werden (Shirvani, Dustary, Shahbaz, Eksiri 2004):
Einlaufteil, Trockenteil und Vorwärmerteil: Es werden sehr verschleißfeste Feuerbeton- und Säuresteine mit einer großen Porosität und feuerfeste Steine oder Betonblöcke verwendet, um dem Abrieb zu widerstehen. In diesem Teil unterliegt der Einlaufring dem Abrieb, und bei sehr langen Drehöfen unterstützt eine Kettenzone diese Beanspruchung. Es gibt auch keramischen Ansatz mit einem guten Widerstand gegen thermische Belastungen.
Die Teile der Anlage sind folgende: Drehrohrofenmantel, Ofenlaufringe, Ofenmantelschüsse (tragen die Laufringe), Laufrollenstation, Antriebsteile, Zahnkranz und Antriebsritzel, Ofeneinlauf- und -auslaufsegment aus Stahlguss, Ofeneinlauf- und -auslaufdichtungen, Heißgaserzeuger und Brenneranlage.
9 Spezifikation der Ansatzeinschätzung im Drehrohrofen
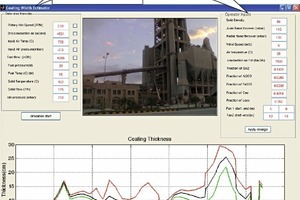
Die grafische Nutzerschnittstelle für die Einschätzung der Ofenstärke wird in Bild 7 gezeigt. In diesem Programm sind einige Daten erforderlich für die Simulation des Ofens und die Berechnung der Ansatzstärke auf der Grundlage eines Wärmenetzwerks, die in zwei Teile untergliedert sind:
9.1 Nutzergrößen
Der Betreiber gibt diese Größen, wie z.B. die Analyse und Dichte des Aufgabeguts, den Verbrennungsluftstrom, Druck und Temperatur beim Brennen, Temperatur und Geschwindigkeit der Umgebungsluft, in die Software ein.
9.2 Online-Größen
Diese Größen, wie z.B. die Temperatur der Außenfläche des Ofens, der Brennstoffstrom, Druck und Temperatur des Brennstoffs, Temperatur des festen Aufgabeguts, Menge des Aufgabeguts und Drehzahl des Ofens, werden dem Programm online aufgegeben. Um diese Daten einzugeben, werden einige Gerätesensoren und Hardware zu diesem Zweck eingesetzt.
Die Drehsensoren werden für die Messung der Temperatur des Ofenkörpers eingesetzt. Diese Sensoren befinden sich auf einem Drehmotor and tasten die Ofenoberfläche mit einer bestimmten Geschwindigkeit ab. Digitale Scanner analysieren die Außenfläche des Ofens über ihre Oberfläche Stein für Stein mit einer Geschwindigkeit von 20 Mal pro Sekunde und einem Blickwinkel von 100 Grad ohne direkte Verbindung von außen. Mit anderen Worten: jeder Stein wird zweimal horizontal pro Umdrehung abgetastet. Diese Verbesserung wurde erreicht dank der Entwicklung der Technologie der Schrägstellung nicht axialer Spiegel, dank besserer Linsen und durch neue Materialien in der Sensorfertigung (Noshirvani 2005).
Entsprechend der Wichtigkeit der Schwankung der Steinstärke in Zementdrehöfen wurde die Schätzfunktion so programmiert, dass die Steinstärke an jeder Stelle berechnet wird, wo Ansatz herunterfällt, und die neue Steinstärke an dieser Stelle bei den nächsten Berechnungen berücksichtigt wird. Dann werden die vergangene Aufzeichnung und der Zustand der Steinstärke im Computer gespeichert, zu dem der Betreiber Zugang hat.
Das Ergebnis der Schützfunktion der Berechnung der Ansatzstärke, die mit drei maximalen, mittleren und minimalen Temperaturen arbeitet, wird in Bild 7 gezeigt
10 Schlussfolgerung
Dieser Artikel beschreibt eine integrierte Reaktionstechnik auf der Grundlage eines mathematischen Modells für die Klinkerbildung in der Zementindustrie. Zuerst wurden einzelne Modelle für den Kalzinator, den Drehofen und seine Flamme entwickelt, die dann kombiniert wurden, um einen integrierten Simulator zu bauen. Dieses Modell basiert auf den Temperaturprofilen von Gas, Feststoff und Wandtemperatur entlang des Ofens. In diesem Artikel werden auch die physikalischen Bedingungen des Ofens, wie z.B. Steinarten, Zusammensetzung des Aufgabeguts und Unterschiede in der Mantelstärke entlang des Ofens, berücksichtigt. Es wurden entsprechende Modelle für die Simulation der Flamme entwickelt, die mit dem Wärmeübergang im Ansatz und im Wandmantel in Berührung kommt. Dieses Modell soll zu einem besseren Verständnis des Einflusses der Betriebsbedingungen auf den Energieverbrauch in einem Zementwerk führen. Verschiedene Wege zur Reduzierung des Energieverbrauchs wurden durch den Computer untersucht. Das Integrandmodell, das entwickelte Programm für den Simulator des Zementdrehofens (RoCKS) und die hier dargelegten Ergebnisse sind nützlich für unser besseres Verständnis und für eine Leistungssteigerung der Klinkerfertigung.
Danksagung
Diese Forschungsarbeit wurde unterstützt durch die iranische Ehdas Sanat Company und Darab Cement Industry.