Research on real-time optimization control algorithm of cement burning system based
on Generative Adversarial Network

1 Introduction

The cement burning system is a typical nonlinear system, which is affected by various factors such as raw and fuel material properties, equipment properties, and distinct operational experiences. It has the characteristics of large time delay, strong coupling, and complex operating conditions. Even though APC technology has alleviated issues caused by variations in raw and fuel materials and differences in operator experience, the set values of controlled variables in APC are still typically determined based on experience, lacking a comprehensive perspective that considers overall economic benefits, product quality, and clinker energy consumption [1]. With the increasing emphasis on green development policies, cement production enterprises face more stringent challenges. The urgent problem to be addressed is how to ensure clinker quality meets specifications, achieves the planned clinker yield, and minimizes energy consumption. In other words, the challenge is to determine the optimal values of controlled variables while considering production constraints [2]. To address this challenge, experts across various fields have initiated extensive research and experiments.

For instance, in the mineral powder grinding process, an application of the constraint RTO algorithm based on linear programming has been proposed in [3]. While this approach has addressed some limitations of APC, it still suffers from the use of static models. This results in the system requiring time to reach a steady state before the next optimization can be performed after adjusting set values. To enhance the dynamic characteristics of the RTO algorithm, numerous data-driven models and algorithms have been proposed and utilized to address this issue. These models encompass regressive models [4], neural network models [5], and various deep learning models [6]. Notably, the aforementioned methods primarily operate in an open-loop manner when addressing real-time optimization problems, and they still exhibit shortcomings in closed-loop control processes.

 In the cement production process, frequent variations in operating conditions result in different distribution laws for each condition, leading to dynamic changes in the statistical characteristics of data. The data model established by the aforementioned method is susceptible to mismatch with the operating condition data [7-10]. Typically, when optimizing production indicators, these methods require real-time determination of appropriate unit process operation indicators, which is challenging in the cement production process. Due to combustion chemical reactions, many reaction processes are opaque, and most process indicators rely on expert knowledge and manual experience. In practical applications, these methods lack sufficient accuracy [8]. Furthermore, the complexity of the cement production process and the digital level result in abnormal value contamination in the collected production data. These contaminated data may lead to unreliable model estimates and necessitate accurate and dependable data cleaning techniques to mitigate these risks [11]. Although the data-driven control method can develop models and controllers for non-transparent systems [12-13], conventional data modeling techniques cannot fully accomplish the aforementioned processes. In the face of numerous complex control processes in industrial settings, more robust data processing and modeling strategies are necessary to improve the accuracy and reliability of the model. Consequently, reinforcement learning (RL) technology has been introduced for data-driven optimization [14]. RL [15-16] is a technique that directly computes process control using data and does not require identifying the process dynamic model. It can optimize user-defined objectives [17-18]. Similarly, the GAN [21-22] algorithm can optimize target optimization through a game between generators and discriminators, without the need to identify the process dynamic model. Compared to RL methods, the GAN algorithm can generate and validate future optimized process data based on current production process data. They can address the issue of insufficient required data samples in the control process of the cement production industry, and possess greater application advantages [23-24].

The research conducted by the aforementioned experts and scholars has provided valuable insights in addressing the challenges faced by cement enterprises. However, the proposed methods are primarily suited for static optimization problems and do not account for the frequent variations in production conditions. They are not well-suited for dynamic optimization processes. Furthermore, despite the utilization of advanced data modeling techniques, they lack comprehensive analysis of practical issues in cement production. These approaches do not effectively address the problem of insufficient observed sample data in optimization problems nor fully tackle the economic optimization concerns in the production process. They do not align with the green, economic, and low-carbon development requirements of cement enterprises. Therefore, the authors aim to optimize objectives of clinker quality, energy consumption, and clinker yield based on the GAN algorithm. A multi-objective loss function is constructed to train the optimization model which will calculate economic, scientific, and effective APC controlled variable target values. This ensures that cement production consistently operates at the optimal economic benefit point.

2 Real-time optimization and control problem

analysis of cement burning system

The APC system is a widely utilized control system in cement production. Operators initially set process control indicators manually based on production requirements, which include not only conventional controlled variables like temperature, pressure, and flow rate but also performance indicators and constraints. Subsequently, the controller models receive the set values of the process control indicators and achieve overall dynamic control of the entire production process through control strategies such as model predictive control and fuzzy control. However, due to the influence of complex internal and external factors, APC systems often encounter issues such as inefficient allocation of economic resources, excessive reliance on the experience of commissioning experts, and a lack of scientific management decisions for production activity objectives. In this context, the RTO algorithm is proposed to address these issues.

The RTO algorithm is a process that integrates technical knowledge with production data to monitor real-time variations in the properties of raw materials and fuels on site. With the objective of optimizing production costs while adhering to technological and equipment constraints, it utilizes mathematical models, mechanism models, and efficient optimization control techniques. By integrating with APC for online closed-loop control, the RTO algorithm achieves real-time optimization of APC controlled variables, ensuring that the production process consistently operates at an optimal state of efficiency, low consumption, and safety. The primary challenges in analyzing RTO control problems reside in three aspects:

(1) How to determine the data distribution of clinker quality, yield and energy consumption under various production conditions;

(2) How to combine the mechanism model with data models to establish multi-objective loss functions;

(3) How to design GAN game strategies to perform real-time optimization calculations on APC controlled variables.

In the following sections, the methods and approaches utilized in this paper to address the aforementioned challenges will be introduced and implemented.

3 Preprocessing production data

and cluster analysis

The present study focuses on the development of the RTO algorithm for the cement burning system, utilizing the GAN algorithm. This approach involves the application and analysis of production process data, quality data, and energy consumption data. However, the field is impacted by various factors, including the accuracy of sampling equipment, stability of data transmission, and human interference in chemical test data. As a result, the analysis data may contain missing values and abrupt abnormalities, necessitating the use of data preprocessing techniques to generate ideal analysis data.

The cement production process is affected by various factors, such as the properties of raw materials, operating variables, and equipment operating conditions, leading to frequent switches in production conditions. Under different production conditions, there are differences in the distribution, correlation, and time delay relationships of production process data, which present optimization opportunities for clinker quality, yield, and energy consumption. To identify reasonable data distributions of production process data and control indicators under various operating conditions, it is essential to determine the operating conditions. The researchers choose to accomplish data state identification and analysis based on the K-means [25] clustering method under different operating conditions. The modeling process is outlined as follows:

(1) Data Preparation

A set of state variables X = {x1, x2, …, xn} that reflect the production process of the cement burning system is selected. The set of clinker quality, clinker yield and clinker energy consumption in the same time period as the state variables X is represented by Y = {q, o, e}. The state variables X follow a distribution px.  The data X and Y are preprocessed and analyzed, including data alignment, removal of shutdown data, outlier exclusion, smoothing, etc., to obtain clean modeling datasets Xc and Yc.

(2) Data Preprocessing

Abnormal data is commonly encountered in the distributed control system (DCS) or other database, making it unsuitable for model construction or statistical analysis. Therefore, an efficient method is required for data outlier elimination. Traditional techniques such as gaussian denoising and median filtering often possess numerous limitations. The wavelet theory, developed to meet to the demands of time-frequency localization, possesses adaptive and mathematical microscopic properties, making it particularly well-suited for the processing of non-stationary and nonlinear signals [26].

Orthogonal wavelet decomposition exhibits the capability of time-frequency local decomposition. After wavelet decomposition, the majority of wavelet coefficients with relatively large amplitude correspond to useful signals, while coefficients with smaller amplitude are typically noise. In other words, the wavelet transformation coefficient of a useful signal is generally greater than that of noise. The wavelet threshold denoising method involves identifying an appropriate threshold value. Wavelet coefficient greater than the threshold are retained, while those smaller than the threshold are considered outlier data and removed. The useful signal is then reconstructed using the processed wavelet coefficients.

(3) Cluster Analysis

The modeling data Xc is inputted into the K-means model for cluster modeling, with the initial number of cluster categories set to K. The silhouette coefficient is used as the clustering evaluation index to determine the optimal number of cluster categories K for the clustering effect. The set of cluster labels for each working condition data is represented as C. 

Based on the clustering results of production process data, the corresponding clinker quality, yield and energy consumption data for each subset in C can be identified. The lower and upper bound ranges of clinker quality, yield, and energy consumption data for each category are calculated using the probability density distribution statistical method, and the distribution interval range J of various production indicators is obtained. The J can be expressed as follows:

⇥(1)

In formula (1), K represents the number of clusters, i represents the i-th cluster. {qⁱ_min,oⁱ_min,eⁱ_min} represents the lower limit of clinker quality, yield, and energy consumption, while {qⁱ_max,oⁱ_max,eⁱ_max} represents the upper limit of clinker quality, yield, and energy consumption. When the cement burning system is operated at maximum yield, optimal quality and minimum energy consumption, it can be indicated that the operation is under the optimal operating condition.

4 Real-time optimization control model

construction and solution

4.1 Construct the Generative Adversarial Network model

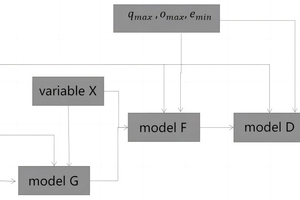
The conventional GAN model consists of a genera-tive model and a discriminative model. To fulfill the real-time optimization control requirements of maximum yield, optimal quality, and minimum coal consumption in a cement burning system, a regressive model is integrated into the network. The regressive model is employed to perform multi-objective prediction regression on the output of the generative model and process variables with respect to maximizing yield, optimizing quality, and minimizing coal consumption. The structure of the GAN model constructed using this approach comprises a generative model G, a discriminative model D, and a regressive model F. The structure diagram is illustrated in Figure 1 as below:

4.1.1 Construct the generative model

The input of the generative model G comprises the state variables X, the random variables Z, and the clustering categories C. The random variables Z are obtained by randomly sampling from the distribution px. The generative model G is utilized to generate the setpoint values G(Z, C, X) = x_i^sp for each state variables X, where i = 1, 2, … n. Here, G(Z, C, X) represents the output of the generative model G, n denotes the number of state variables X, and X_i^sp signifies the setpoint values of the i-th state variables, which is then fed into the APC control loop.

4.1.2 Construct the regressive model

The inputs of regressive model F consist of the state variables X, the clustering categories C, and data G(Z, C, X) generated by the generative model G. The output of regressive model F is the actual optimal clinker quality q_max, maximum clinker yield o_max, and minimum clinker energy consumption e_min corresponding to the categories C in the same time period. The regressive model F is implemented using a multi-output neural network, with the following output definitions:

⇥(2)

In which NW_wf represents the functional expression of the regressive model F.

4.1.3 Construct the discriminative Model

The inputs of the discriminative model D consist of three parts: categories C, the set f  composed of the predicted clinker quality q_max, yield o_max and energy consumption data e_min obtained from the regressive model F, and the set f corresponding to the actual optimal clinker quality q_max, maximum clinker yield o_max and minimum clinker energy consumption e_min corresponding to the categories C, as shown below:

⇥(3)

⇥

⇥(4)

4.2 Build the multi-objective loss function

Generally, the learning process of GAN model involves the following steps:

(1) Under the premise of fixed generative model G, the discriminative model D and the regressive model F will be optimized.

(2) The discriminative model D is trained using the minimum cross-entropy method to optimize the loss function and find the solution.

(3) The loss function of regressive model F is constructed by using the mean square error between the predicted and actual values to establish optimization iteration.

(4) Among these, constructing the loss function for the discriminative model D is particularly crucial. To establish an effective approach that enhances the discriminative model D’s correct judgments, it is essential to consider not only the similarity of distributions between real predicted clinker quality, yield and energy consumption data but also the zero-sum game between the generative model G and the discriminative model D. The above predicted clinker quality, yield and energy consumption data from the output of the regressive model F based on the generated data as model input.

Therefore, the authors propose the following multi-objective loss function for the discriminative model D:

⇥ (5)

In this context, E(·)represents the expectation value calculation, p(·)represents the data distribution, and D(f ) represents the distribution of real data from optimal clinker quality, maximum clinker yield, and minimum clinker energy consumption. D(f  ) also denotes the predicted data distribution output by the regressive model F.

The discriminative model D is utilized to accurately discern whether f and f are consistent, while the objective of the generative model G is to generate data G(Z, C,K) representing the optimal operating state to ensure that the predictions outputted by the regressive model F align with the optimal clinker quality, maximum clinker yield, and minimum clinker energy consumption state. Consequently, the loss function of the generative model G is indicated as loss_G = -loss_D. So, the overall loss function of the GAN model is shown as below:

⇥(6)

4.3 Optimize the solution

Based on the GAN model structure established in Section 4.1 and the loss function constructed in Section 4.2, the process of training and optimizing the GAN model is as follows:

The authors choose to train the generative model G with the inputs of state variable X, random variables Z and categories C. The generative model G generates data G(Z, C, X), reflecting the operating state of the cement burning system. The data G(Z, C, X), combined with state variables X, are fed into the regressive model F. The output of the regressive model F is close to the optimal clinker quality q_max, maximum clinker yield o_max, and minimum clinker energy consumption e_min. At this point, if the data generated by the generative model G indicates that the production is stable at the optimal state, the discriminative model D will label such data as 1. Otherwise, if the data generated by the generative model G inputted into the regressive model F, results in outputs significantly different from the optimal clinker quality q_max, maximum clinker yield o_max, and lowest clinker energy consumption e_min, the discriminative model D will label such data as 0. The discriminative model D is utilized to accurately determine whether the data generated by generative model G meets the requirements of optimal clinker quality, maximum clinker yield and minimum clinker energy consumption. And the generative model G is utilized to ensure that the generated data G(Z, C, X) maintains the optimal operating state. Through fighting against each other and continuously optimization between the discriminative model D and generative model G, the performance of both is continuously enhanced. When the discriminative ability of the final discriminative model D improves and can accurately determine data source, and when the predicted output of the regressive model F is close to the actual value, it is considered that the generative model G has learned the setpoint values of state variables X corresponding to the optimal production state at categories C. The set values of state variables X, obtained through the aforementioned method, are inputted into the APC control loop to achieve dynamic adjustment of variables by the APC control loop, ensuring that the cement burning system always operates around the optimal production mode.

5 Example analysis

Taking the application effect of a cement plant with a production capacity of ten thousand TPD in China as an example, this method is demonstrated and explained.

The state variables X that reflect the clinker quality, clinker yield and clinker energy consumption of the cement burning system are selected, which include the outlet temperature D_T of the decomposition furnace, the feeding temperature of C5, the current of the lifting machine into the kiln, the current of the kiln, the temperature of the burning zone, the NO_x content in the tail flue gas chamber of the kiln, the temperature of the secondary air, the temperature of the cold machine for discharged clinkers from the grate, and the temperature of the fire observation TV at the head of the kiln, etc. The corresponding symbols of each variable are shown in Table 1.

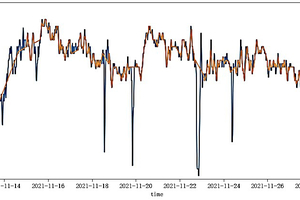
The chosen data sampling interval is set to 15 min, and a total of 23889 data samples are collected. The valid operating data are selected from the data with kiln current greater than 30 and clinker production rate in the range of (40, 150). After shutdown processing, a total of 12,524 data samples are obtained. The data trends from 11 -16 April 2022 are shown in Figure 2.

Prior to constructing the GAN model, abnormal data are processed using wavelet transform. The processed result is shown is Figure 3. The blue curve in Figure 3 represents the trend of the original kiln current, while the orange curve represents the trend of the kiln current after outliers are removed. By analyzing the above results, it can be observed that the wavelet transform method effectively identifies and eliminates abnormal data, while also smoothing the data.

Through multiple experimental comparisons, the production conditions are divided into 5 optimal conditions by the K-means clustering model. For each of the 5 clusters, the corresponding clinker quality, clinker yield, and clinker energy consumption data are selected. The lower and upper ranges for each of these parameters are calculated, as shown in Table 2.

The regressive model F in the presented GAN model is set up with 13 input neurons and 3 output neurons. The backbone of the regressive model F utilizes the ResNet structure of residual networks. The batch size is set to 64, and the Leaky ReLU function is used for neuron activation.

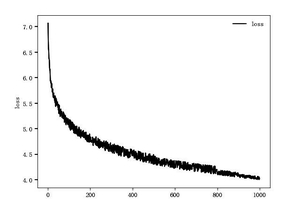
The GAN model optimizer is chosen as Adam, and the training loss curve is depicted in Figure 4.

The optimized GAN model is deployed on-site, and the model makes predictions every 15 minutes. In each cycle, it reads the real-time values of six controlled variables from the data source. It predicts the category to which the current controlled variables belong through an operating condition clustering model and finds the optimal clinker quality, maximum clinker yield, and minimum clinker energy consumption data for that category. The real-time values and categories of the controlled variables are inputted into the generative model, and the data generated by the generative model are set as the input of state variables X into the APC loop. After APC system deploy the set point of X by the output from the real-time optimization control system instead of manual experience, the optimization effects obtained significant boost, the compared results are shown in Table 3.

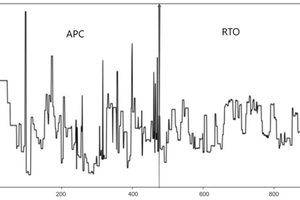
The reduction of clinker standard coal waste in the calcination system is illustrated in Figure 5.

The improvement effect of the qualified rate and stability of clinker quality after the sintering system is shown in Figure 6.

6 Conclusion

The research and development of the RTO algorithm for the cement calcination system based on the GAN model provides a new solution for parameter setting in the APC loop. It has solved the data deficiency problem in the cement plant through generative modeling. By incorporating a regressive model into the original GAN model structure, the small sample prediction problem can be effectively addressed. The zero-sum game between generative modeling and discriminative modeling effectively achieves parameter optimization in the optimal production mode, which has high application value in cement. The presented RTO algorithm, of the cement calcination system based on the GAN model has addressed the long-standing issue of relying on the manual experience for the set values of controlled variables. It considers multiple factors such as overall economic benefits, product quality, and clinker energy consumption. Additionally, it can overcome interference factors caused by frequent changes in operating conditions during cement production. By implementing this method, the efficiency of control loop commissioning is significantly improved, with an average automation commissioning rate of over 96%. This contributes to a reduction in the standard coal consumption of clinker by 3.03%, an improvement in the stability of clinker quality by 39.3%, and an increase in the feeding amount of the calcination system by 1.9%. By on-site experiment analysis, this RTO algorithm based on GAN model is an effective method for APC parameter optimization.