Influence of material properties on the decomposition time of limestone under shaft kiln conditions
The influence of the material properties on the decomposition of limestone particles under shaft kiln conditions has been investigated. Limestone particles are assumed to be spherical particles and the shrinking core model has been applied. In counter-flow single-shaft kilns with high temperatures, the thermal conductivity of the lime has the dominant influence with up to 90 % for large particles. In parallel-flow regenerative (PFR) shaft kilns with lower temperatures, the reaction coefficient and the equilibrium pressure also have a significant influence in addition to the thermal conductivity. These three material properties can fluctuate up to a factor of two depending on the origin of the limestone.
1 Introduction
The decomposition of limestone is an endothermic topochemical reaction:
CaCO3 + ΔHR = CaO + CO2
(solid) (reaction enthalpy) (solid) (gaseous)
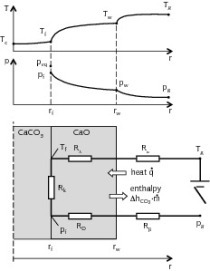
The calcination process can be explained by using a partially decomposed piece of carbonate [1, 2]. The calcination profiles of CO2 partial pressure and temperature are shown in Figure 1. The specimen comprises a dense carbonate core surrounded by a porous lime layer. In the kiln the combustion gas with the temperature Tg transfers heat by convection (symbolized by α) to the solid surface with the...
1 Introduction
The decomposition of limestone is an endothermic topochemical reaction:
CaCO3 + ΔHR = CaO + CO2
(solid) (reaction enthalpy) (solid) (gaseous)
The calcination process can be explained by using a partially decomposed piece of carbonate [1, 2]. The calcination profiles of CO2 partial pressure and temperature are shown in Figure 1. The specimen comprises a dense carbonate core surrounded by a porous lime layer. In the kiln the combustion gas with the temperature Tg transfers heat by convection (symbolized by α) to the solid surface with the temperature Tw. The heat is conducted through the lime layer to the reaction front with the temperature Tf. As the reaction enthalpy is many times greater than the internal enthalpy, the heat flowing further into the core is negligible during the reaction. Therefore, the core temperature is similar to the front temperature. At the front, the chemical reaction (k) of the decomposition takes place, for which the driving force is the deviation of CO2 partial pressure from the equilibrium pressure (peq- pf ). The released CO2 diffuses (DP ) through the porous lime layer to the surface and finally passes by convection (β) to the surroundings where the CO2 partial pressure pg exists. The four physical transport processes and the chemical kinetics involved are therefore interconnected. These can be explained as a series of resistances as shown in Figure 2. Heat flows to the reaction front and flows out with the carbon dioxide as decomposition enthalpy. The limestone calcination process must overcome all these resistances. Hence the time of calcination is expressed as sum of these resistances.
2 Decomposition in industrial shaft kilns
2.1 Process conditions
First, the process parameters for the calcination of limestone particles undergoing decomposition in industrial shaft kilns are characterized. The mean temperature in the reaction zone of the PFR kilns is in the range of 900 – 1200° C [3, 4], whereas counter-flow single-shaft kilns are operated at much higher temperatures up to 1600° C [5, 6, 7]. The volume flow in the reaction zone slightly increases due to the decomposition reaction. Depending on the energy consumption and excess air number, a typical mean value of 12 000 m³/(m² h) at STP is taken [5, 6]. The superficial velocity of the gas flow is 0.7 m/s and void fraction of the kiln is 0.4.
2.2 Determination of heat and mass transfer for the kiln
The heat transfer in a shaft kiln (packed bed) is dominated by convection. One approach to estimate the convective heat transfer coefficient (α) in a packed bed is given as [8]:
⇥(1)
where ψ is the void fraction of the packed bed. The Nusselt number and Reynolds numbers are defined respectively as:
⇥(2)
where d is the size of the particle, λg is the gas thermal conductivity, ν is gas kinematic viscosity and w is the empty kiln gas velocity, which is called the superficial velocity. This velocity is determined by:
⇥(3)
where wSTP is the velocity at STP (standard temperature and pressure) condition, ρ and ρSTP are the densities at temperature T and at STP respectively. Here VSTP is the gas volume flow at STP and AF is the cross-section area of the kiln.
In the simulation of limestone decomposition, the convective mass transfer of the produced CO2 into the gaseous ambience must be calculated. With analogy to heat transfer, the mass transfer coefficient of CO2 from the limestone surface to the gas, β, can be calculated from the Sherwood function.
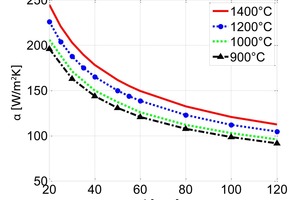
Figure 3 presents the convective heat transfer coefficient in respect of particle size for different kiln gas temperatures. It strongly decreases with size of the particles with the power of approximately 0.5. The gas temperature only has a slight influence.
2.3 Resistances
The resistances for the heat transfer and thermal conduction are given as [1, 9]:
and ⇥(4)
Here α is the heat transfer coefficient, λ the conductivity, ΔhR the reaction enthalpy (168 kJ/kmol, 3820 kJ/kg CO2), KCO2 the CO2 content in the limestone (1190 kg CO2/m³ limestone) and d the particle diameter. The resistances for the reaction, diffusion and mass transfer are
⇥and
⇥(5)
Here Rc is the gas constant of the carbon dioxide, β the mass transfer coefficient, Dp the pore diffusion coefficient and k the reaction coefficient.
The thermal conductivities of limes from different origins are determined in [10, 11]. The values fluctuate between 0.4 and 0.9 W/(mK). The reaction coefficients of different limestones are determined in [12]. The values fluctuate again by a factor of more than two.
The resistances for the heat transport and the mass transport are connected with the equilibrium pressure
⇥(6)
which is dependent on the temperature at the reaction front. This pressure also depends on the origin of the limestone [13]. The pressure can fluctuate by a factor of 1.4, which results in decomposition temperatures in pure carbon dioxide at one bar between 900 °C and 935 °C.
The influence of the material properties on the decomposition are discussed in the following sections.
3 Sensitivity
3.1 Definition
Sensitivity to calcination is defined as the extent of influence caused by each of the resistances on the time of calcination. It is formulated as:
Sensitivity where is the sensitivity
in respect of the resistance i.
The influence of this change on the calcination is numerically computed and discussed for calcination at different gas temperatures between 900 °C and 1400 °C. For all the simulations at these temperatures, enthalpy of reaction is 168 kJ/mol, the equilibrium temperature is considered as 910 °C, tortuosity is 2, porosity is 0.5, density of the limestone is 2700 kg/m³, reaction coefficient 0.003 m/s and ambient partial pressure of CO2 gas in the kiln is 0.3 bar.
3.2 Thermal conductivity
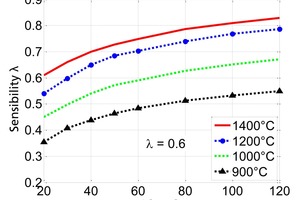
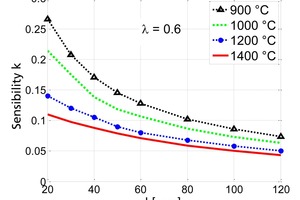
Figure 4 shows the sensitivity of the thermal conductivity in respect of the diameter of the particle for shaft kilns which are operated at gas temperatures 900 to 1400 °C. The sensitivity increases significantly with the particle diameter. The sensitivity also increases with the gas temperature. However, its influence becomes weak for values above 1200° C. The decrease of the influence of the conductivity for lower gas temperatures is due to the increasing sensitivity of the reaction coefficient as shown later. The sensitivity of the thermal conductivity is in the range of 0.5 to 0.8 for typical kiln temperature above 1000 °C. This demonstrates that the thermal conductivity is the most dominant material property.
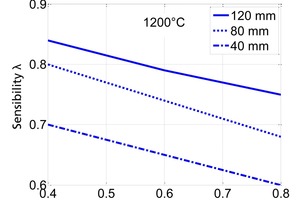
In Figure 4, a mean value of 0.6 W/(mK) is used for the conductivity. Figure 5 shows the sensitivity of the range of possible values. The lower the conductivity is the larger is its influence.
3.3 Heat transfer
Figure 6 shows the sensitivity of the heat transfer. It decreases with the particles’ diameter. That is surprising, because the heat transfer coefficient decreases with the particle diameter as shown in Figure 3. Therefore, its influence would be expected to increase. However, the sensitivity of the conductivity also increases with the particle diameter. Because this sensitivity is more dominant, the sensitivity of the heat transfer decreases with the diameter.
The sensitivity decreases slightly at lower temperatures. This is due to the increasing sensitivity of the reaction and diffusion.
3.4 Mass transport
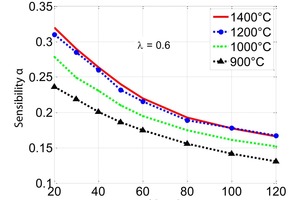
Figure 7 shows the sensitivity of the chemical reaction of the decomposition. It increases the smaller the particle diameter is and the lower the temperature becomes. Therefore, in PFR kilns the influence of the reaction coefficient can reach 20 %.
Figure 8 describes the sensitivity of the diffusion. Its values increase with the diameter similar to the thermal conductivity. At temperatures above 1000 °C, the influence is very small. For large particles and temperatures around 1000 °C, such as in PFR kilns, the influence can reach 15 %.
The mass transfer coefficient exhibits almost no influence on the calcination. At a low temperature of 900 °C, the sensitivity is found to have a maximum value of around 0.7 % for 20-mm-size particles, hence it is not plotted.
3.5 Equilibrium temperature
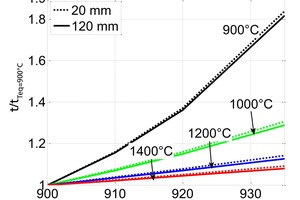
The equilibrium temperature is defined as the temperature at which the calcination begins in pure carbon dioxide at a pressure of 1 bar. It depends on the origin of the limestone and is in the range from 900 °C to 935 °C [11, 13]. Therefore, at a given temperature the equilibrium (decomposition) pressure can change by 40 %. Various simulations are carried out with limestone of sizes 20 mm and 120 mm and at different possible equilibrium temperatures between 900 and 935 °C. In all these simulations, the time for complete calcination is calculated and its ratio with the time for calcination at equilibrium temperature of 900 °C is formed. This ratio versus the equilibrium temperatures is plotted in Figure 9. From this figure, it can be seen that as the equilibrium temperature increases, the time of calcination increases. This effect is stronger for lower calcination temperatures. The effect of particle size is not so significant. In PFR kilns with temperatures around 1000° C the difference in the decomposition time can reach 30 %.
4 Conclusion
The thermal conductivity has the strongest effect of all material properties and process parameters on the decomposition time. For high temperatures and large particles, the sensitivity can reach 80 %. The second ranking is the heat transfer coefficient. At high temperatures, like in counter-flow single-shaft kilns, the CO2 mass transport is negligible. Only in PFR kilns with temperatures around 1000° C, the sensitivity of the reaction coefficient can reach up to 20 % for smaller particles. As a consequence, to determine the material properties of individual limestones, large particles at high temperature must be calcined for the determination of the thermal conductivity and small particles at low temperatures must be decomposed to determine the reaction coefficient.

Überschrift Bezahlschranke (EN)
tab ZKG KOMBI EN
This is a trial offer for programming testing only. It does not entitle you to a valid subscription and is intended purely for testing purposes. Please do not follow this process.
This is a trial offer for programming testing only. It does not entitle you to a valid subscription and is intended purely for testing purposes. Please do not follow this process.
tab ZKG KOMBI Study test
This is a trial offer for programming testing only. It does not entitle you to a valid subscription and is intended purely for testing purposes. Please do not follow this process.
This is a trial offer for programming testing only. It does not entitle you to a valid subscription and is intended purely for testing purposes. Please do not follow this process.