Multi-criteria decision-making model for establishing the optimal typology for clinker storage silos

1 Introduction

The contribution of the concrete and cement industry to the economy represents a total production value of 74 billion € and a value added of 22 billion €, accounting for 366000 jobs [1]. In 2020 a production of about 242 million tons of clinker is estimated. Large store structures play an important role in the manufacturing process of cement, ensuring the management of raw and intermediate materials and the storage of the final product. These storage silos are essential to manage the fluctuations between the supply of materials and their implementation in the production process or between the sales of the final product and its production. Hence the correct choice of the appropriate storage system will have a significant impact on the management of production processes and on the economic profits obtained. There are many techniques to determine the pressures exerted by stored materials and to approach the design of silos or its associated mechanical equipment [2-4]. However, there is a research lack regarding the choice of the most appropriate storage typology in each case, as the first and key step to optimal design.

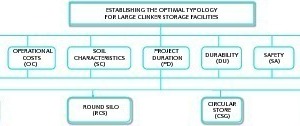
The election of the type of silo depends not only on commensurable criteria, such as the construction cost, but also on intangible and not ­easily quantifiable factors. In this decision-making problem, the project manager generally needs to identify important decision factors and to evaluate their relative importance in order to establish the most preferred facility. The selection of optimal silo typology consists of essential management criterion such as: Construction costs  i.e. , the setting up costs and the necessary  mechanical  equipment for its operation [5-7]; Operating costs, including the costs related to operation and maintenance over the lifetime of the installation itself [8, 9]; ­Operability of material, i.e. the efficiency when loading and unloading the storage facility and its capability to guarantee the stored product quality [10]; soil characteristics, soil properties and its bearing capacity will define the most appropriate storage typology for each location [11, 12]; project duration, it takes into account the period required for the construction and the commissioning [13]. ­Durability of the facility, the capability of the storage system to  resist the damage caused by the aggressiveness of stored material, temperature, friction, etc will determine its lifetime [14]; safety against the risk of damage caused by a structural failure, against unexpected phenomena such natural disasters or operational accidents [15-17]; sustainability, this criteria considers the contribution of the selected type of storage system to environmental sustainability and its effect on the plant as a whole [18-22]; visual impact, assessing the visual effect of the storage facility on the specific environment considered [23, 24].

This paper presents an expert system to determine the optimal silo typology for storing 50 000 tons of cement clinker. Nowadays, common typologies of storage systems are the vertical silos, longitudinal stores, circular stores and clinker domes [25, 26]. Selecting an appropriated solution encompasses an intricate trade-off procedure which requires all the assessment criteria to be taken into account simultaneously. The expert system proposed to overcome such heterogeneous criteria is a hybrid method combining the Analytical Hierarchy Process (AHP) with the Delphi method and the VIKOR technique. The AHP method, proposed by Saaty [27], is an effective method for solving multi-criteria decision-making problems that has been applied in several areas of construction management [28, 29].

The AHP is a theory of relative quantification on absolute scales able to address intangible criteria and based on paired evaluation assessment of knowledgeable experts [30, 31]. The main concern of the mathematics of the AHP is the quantification of intangibles as this paper will show. Experience, gained over the years with the AHP methodology in several decision-making spheres, shows that it is an appropriate technique for structuring the relevant knowledge concerning consensus in complex multicriteria problems. The Delphi method is suitable as a means and technique for consensus-building by using a set of questionnaires to gather data from a panel of selected experts [32, 33]. The Delphi technique is performed to facilitate an ­efficient survey from the panel of experts.

At last, the VIKOR method finds a compromise resolution in decision-making dilemmas, involving non-commensurable and conflicting criteria, that is closer to the ideal and the solutions are evaluated in accordance with all established factors [34, 35]. A stability analysis is performed; also the achieved compromise solution gives a maximum utility of the majority, and a lowest individual regret of the opponent.

2 Structuring of the clinker storage decision

as a hierarchy

The Industrial Emissions Directive 2010/75/EU, ­establishes regulations on integrated prevention and control of pollution emanating from industrial activities. On the other hand, according to Regulation EC 1272/2008, the clinker diffuse dust generated by high volume stocks is harmful to human health as it can cause irritation and injury.

In 2013, The European Commission Decision 2013/163/EU lays down the best available techniques under the aforementioned Directive 2010/75/EU on industrial emissions for the production of cement. For clinker storage, clinker silos and closed fully automated raw material storage areas are considered the most efficient solution to the problem of diffuse dust generated during filling operations.

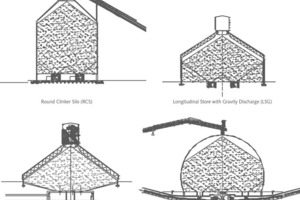
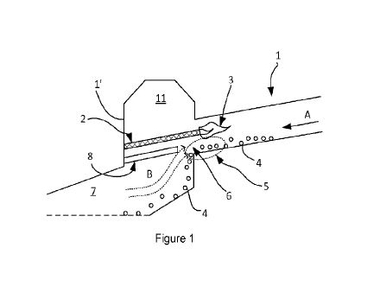
There are several closed-form solutions that achieve the recommendations of these directives, according to the Joint Research Center [36], the best available techniques for the cement industry applied nowadays for the storage capacities commonly projected are: Round Clinker Silo (RCS); Longitudinal Store with Gravity Discharge (LSG); Circular Store with Gravity Discharge (CSG) and Clinker Storage Dome (CSD). The Project contractor must choose the optimal storage building among these four systems. Figure 1 shows diagrams of these facilities whose advantages and disadvantages are analyzed afterwards.

A round clinker silo is a vertical cylindrical silo, whose walls are built with post-tensioned concrete for this storage capacity. The clinker feeding is located on the metallic deck, while the discharge is carried out by gravity through extraction tunnels equipped with conveyors. This system allows a high live stock and requires good soil characteristics. Problems with ground vibrations may occur during clinker withdrawal from the silo at certain silo levels [37].

In the longitudinal store the bulk material is placed on the floor in long prismatic piles. Nowa­days, storing clinker in enclosed structures is more usual due to environmental emission restrictions [38], therefore it is necessary to construct closed warehouses to store the material. The material is loaded with a lateral stacker, or by a mobile band from above. To remove the material, we can use extraction tunnels or a mechanical reclaimer with scrapers. This storage system often has higher investment costs than other solutions.

The circular stockpile is the simplest solution for storing free-flowing materials [39]. In a circular store clinker is stored in a conical pile and reclaimed through subterranean tunnels with hoppers and conveyors. Since the drop height of the material is considerable when stored in a conical pile, large amounts of dust are produced if it is not covered. A metallic structure is usually constructed to enclose the material. This system allows a high live stock.

Clinker storage domes are also used to store clinker. Compared with other silos, dome s­ilos have the largest volume in relationship to their floor-space [40]. The floor of this type of silo is flat; there are structures with a profile that closely follow the shape of the stockpile, so commonly the parabolic profile is preferred. This is an economical way to store. The dome may also be supported on a concrete perimeter wall to increase its storage capacity.

A panel of civil engineers has been created for the decision making, all having worked on or studied problems related with the cement industry or the material storage systems. The hierarchy of this decision-making problem was elaborated based on the criteria suggested by the experts’ opinions using a Delphi technique. Each expert was asked to identify possible factors to consider in the decision process, reaching the final hierarchical tree structure shown in Figure 2.

3 Pairwise comparison matrix for the criteria

In accordance with the Delphi method, we asked a group of experts to assess the importance of the decision criteria. The key step in determining the priorities of elements in a decision problem is to make pairwise comparisons, that is to say, to evaluate the elements in pairs against a given factor. The Delphi process accomplishes interaction among the panel of expert engineers with anonymous feedback, while AHP is applied to divide the overall decision making into smaller judgment components [41].↓

⎡ 1 0.7628 1.0000 0.6123 4.1108 1.7321 1.7321 1.3110 2.4526 ⎤

⎢ 1.3110 1 1.3110 0.8027 4.7452 2.0189 1.9037 1.9332 3.2154 ⎥

⎢ 1.0000 0.7628 1 0.5774 3.8386 1.8228 1.7188 1.3797 2.3126 ⎥

⎢ 1.6332 1.2457 1.7321 1 4.8247 2.5150 2.4526 1.9840 3.1356 ⎥

A = ⎢ 0.2433 0.2107 0.2605 0.2073 1 0.3385 0.3653 0.3033 0.5173 ⎥⇥(1)

⎢ 0.5774 0.4953 0.5486 0.3976 2.9542 1 1.0000 0.9502 1.9332 ⎥

⎢ 0.5774 0.5253 0.5818 0.4077 2.7374 1.0000 1 0.7569 1.6207 ⎥

⎢ 0.7628 0.5173 0.7248 0.5040 3.2972 1.0524 1.3211 1 4.2154 ⎥

⎣ 0.4077 0.3110 0.4324 0.3189 1.9332 0.5173 0.6170 0.2372 1 ⎦↓

A matrix is the preferred structure for pairwise comparisons. To construct the matrix of pairwise comparisons, we employ numbers to symbolize the relative importance of one factor or facility over another. Table 1 contains a 9-point linguistic scale of the AHP used for pairwise comparisons. In order to discriminate the intensity of interactions between elements, a scale of nine units has been adopted [42]. The numerically translated assessments are approximations and their adequacy will be analyzed by a test of consistency.

Each engineer performed a pairwise comparison to designate his predilection for each factor; Table 2 shows a particular questionnaire for evaluating main factor with respect to the clinker storage system. The assessment answers can be found in Table 3. As a result, a pairwise comparison matrix for the criteria is constructed aggregating the individual judgments of the panel of experts, using the mean geometric value achieved from Table 3. This matrix A is given by (1).

4 Eigenvector method and consistency analysis

Once the pairwise comparison matrix for the factors (A) is obtained, we synthesize the judgments to get an estimated approximation of the relative priorities of these criteria. According to Saaty [27], the principal eigenvector of A is the desired priority vector v. To find this vector, the linear system Av = lv must be solved.

det A = (A – lI)⇥(2)

As a result, the priority vector of the factors is as follows.

⎧ 0.1336 ⎫

⎪ 0.1698 ⎪

⎪ 0.1327 ⎪ ⎪ 0.1997 ⎪

v = ⎨ 0.0326 ⎬⇥(3)

⎪ 0.0861 ⎪ ⎪ 0.0824 ⎪

⎪ 0.1121 ⎪

⎩ 0.0510 ⎭

In decision-making problems it is important to identify how good the consistency is, because the decision cannot be based on judgments that have such low consistency that they appear to be random. In fact, perfect consistency is hard to reach, however a certain level of consistency in setting priorities is necessary to get suitable results. The AHP method measures whether or not the inconsistency occurs in the evaluation process, in order to guaranty the procedure, since the specialists are commonly not capable of expressing consistent preferences in the event of numerous criteria.

The Saaty’s method evaluates the overall consistency of assessments by means of a consistency ratio (CR). In practice, the value of the consistency ratio should be 10 % or less (CR ≤ 0.1), for order of matrix (n) equal or larger than five. If it is more than 10 %, the answers from the experts may be slightly random and must be reworked. CR is obtained by dividing the consistency index (CI) by the random consistency index (RCI) addressed by Saaty as follows:

CR =  CI⇥(4)

         RCI

In order to calculate the (CI), largest eigenvalue (l_max) of the pairwise comparison matrix (A) is needed. Then, the consistence index (CI) is obtained as follows.

CI = l_max – n⇥(5)

         n – 1

The relative preference rating and consistence evaluation is determined as shown in Table 4.

5 Assessment of the storing facilities

according to criteria

According to AHP method, the next step is to evaluate the priority of facilities with respect to each factor. Another questionnaire is sent to the panel of engineers, it will be applied to assess silos for each criterion. For example, Table 5 shows a particular questionnaire for evaluating facilities using a 9-point scale (see Tab. 1), with respect to an individual factor (CC) to better illustrate the application of the expert system proposed. Each specialist has completed a pairwise comparison to denote his preference for each clinker storage system. After that, a pairwise comparison matrix for the silos is constructed using the geometric mean obtained from all experts. As in the previous section, to obtain the priority vector, the eigenvector method has been used, and a consistency analysis performed for each case. All criteria assessments are analyzed, the assessments for one of these factors (CC) are shown as an example in Tables 6 and 7 and the priority matrix is constructed (Table 8).

After evaluating factors and clinker storage systems, the VIKOR method is applied to find a compromise solution and perform a stability analysis [43]. The closeness of each silo with respect to the ideal storage facility is measured. Initially, we determined the best f_i^* and the worst f_i^- values of all clinker storage factors ratings j = 1, 2, ..., n, where:  f_i^* = max_i {x_ij} and f_i- = min_i {x_ij}. Table 9 presents the results for the ratings f_i^* and f_i^– for the n-factors.

In accordance with the VIKOR technique, we compute the values S_i, R_i and Q_i using the following equations:

 ⇥

S_i = ∑ ⁿ _j = 1 w_j = f_j^* – x_ij⇥(6)

                      f_j^* – f_j^–

⇥

R_i = max_j w_j = f_j^* – x_ij⇥(7)

                        f_j^* – f_j^–

Q_i = y S_i – S^* + (1 – y) R_i – R^*⇥(8)

          S^– – S^*                       R^– – R^*

Where w_j are the weights of factors, expressing their relative importance, and S^* = min S_i,

S^- = max. S_i, R^* = min. R_i, R^– = max. R_i. As well as y is the weight for the strategy of maximum group utility and (1 – y) is for the individual regret, here we apply the “by consensus” value y = 0.5. Next we rank the silos, sorting by the values S, R and Q in decreasing order as shown in Table 10.

The VIKOR method proposes as a compromise solution the clinker storage dome (CSD) which is the best ranked by the measure Q. Moreover, the next two conditions are satisfied.

Acceptable advantage: (Q_LSG – Q_CSD) ≥ DQ

Where the longitudinal store (LSG) is the facility with second position in the ranking list by Q; and DQ = 1/(J − 1); J is the number of storage facilities under study.

Acceptable stability in decision making: clinker storage dome (CSD) must also be the best ranked by S or/and R.

In our case, the reached compromise solution for the optimal clinker storage facility could be accepted because it accomplishes a maximum utility of the majority (characterized by minimum S), and a minimum individual regret (characterized by minimum R).

6 Conclusions

Storage facilities are essential for the management of several production and control stock processes, as well as for the development of large civil engineering construction works. Traditionally, the selection of the facility typology is based on the experience of the project manager, or on purely economic criteria, although it is not necessarily optimal from a global point of view.

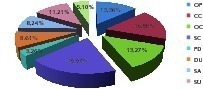
These uncertainties in the choice procedure justify the need for tools to solve the decision-making problem. In the particular case studied, the preferred typology for the storage of clinker is the Clinker Storage Dome (CSD). It is a decision-making problem with intangible and not commensurable factors involved. To resolve the complex problem we consulted to a panel of expert engineers who, using the method Delphi-AHP, have identified and assessed the most relevant criteria for decision-making, Figure 3 presents the weights of each factor.

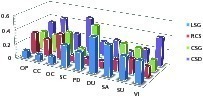
For all these criteria, the alternatives proposed have been compared, Figure 4 shows the weights of each facility for each criterion. And finally, the VIKOR technique has enabled us to select the most preferred solution, guarantying consensus and stability.

Therefore, the problem analyzed in this paper is an example of the reliability of the proposed method for determining the most preferred typology for storing materials, even if intangible and not easily quantifiable factors are involved. This technique can be applied in many other specific problems, adapting in each case the most important selection criteria for decision-making. In addition to this, the method is not restricted to the field of storage structures, but also presents a higher potential and can be applied in many different decision-making problems in civil engineering and management.